5 (1217)

■)0' ^J r-i

Ciągi liczbowe

raniczony, tzn.

i wyrazy leżą między dwiema t ograniczony, nazywamy nie-

Podstawowe określenia

V    fl

^a) ^an = -o -rr;

7^ + 1

i mr c) c_n — n Jsm —

e) e_n — v n² + n sin n

47

b) b_n — 4 — 3 cos n; d) = (—2)ⁿ;

n; f*) U = 1 +    ^ + • • • +

aiczonego.

tak dobrać stale m i M,

rożna

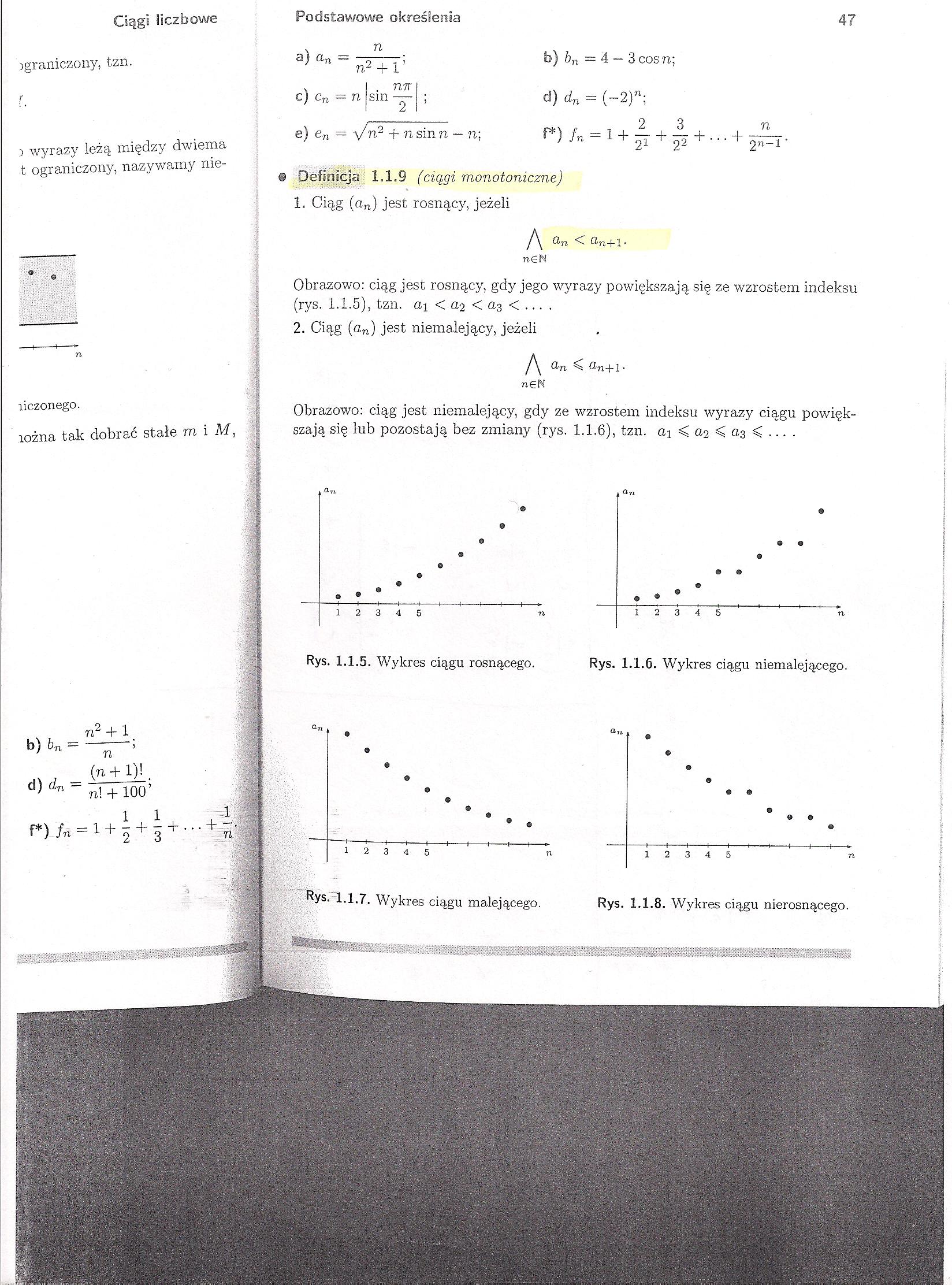
@ Definicja 1.1.9 (ciągi monotoniczne)

1.    Ciąg (a_n) jest rosnący, jeżeli

n ^ ®n+l>

Obrazowo: ciąg jest rosnący, gdy jego wyrazy powiększają się ze wzrostem indeksu (rys. 1.1.5), tzn. a\ < a~i < 0,3 < ... .

2.    Ciąg (o,_n) jest niemalejący, jeżeli

yy C Un+l-

ngN

Obrazowo: ciąg jest niemalejący, gdy ze wzrostem indeksu wyrazy ciągu powiększają się lub pozostają bez zmiany (rys. 1.1.6), tzn. a\ < <22 < az < ... .

2    3    4    5

Rys. 1.1.5. Wykres ciągu rosnącego.

Rys. 1.1.6. Wykres ciągu niemalejącego.

n² + 1.

b) b_n = _n ’

(n + l)¹- ,

^d) ^{dn =} n\+ 100’

f*) U = 1 + \ + 5 ⁺ • ■ •⁺

1    2    3    4    5

1    2    3    4    5

Rys. 1.1.7. Wykres ciągu malejącego.

Rys. 1.1.8. Wykres ciągu nierosnącego.