62 (102)

62 Stanisław Szuba

/(<)- —+V[a„ cos (H0f) +i_nsin (mću/)],

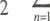
(9.2)

gdzie a_n i b_n są odpowiednio parzystymi i nieparzystymi współczynnikami Fouriera, a co jest częstotliwością kołową (równą 2tiIT) zwaną częstotliwością podstawową.

Dla przykładowej funkcji na rysunku 9.1 wartości kilku początkowych współczynników Fouriera zawiera tabelka poniżej; wszystkie pozostałe są zerowe.

Częstotliwości kołowe składowych harmonicznych (widoczne w argumencie funkcji sin i cos) są całkowitą wielokrotnością («) częstotliwości podstawowej, np. co, 2(o, 3co...» a okresy składowych harmonicznych sąn-krotnie mniejsze od okresu podstawowego. Składowa o częstotliwości kołowej nco (o okresie Tin) nazywa się M-tą harmoniczną, z wyjątkiem n = 1 (podstawowa) i n = 0 (stała).

Amplituda M-tej harmonicznej ^4„ jest dana wyrażeniem:

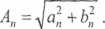
(9.3)

Zbiór amplitud wszystkich harmonicznych tworzy widmo fourierowskie, przedstawiane najczęściej w postaci wykresu słupkowego lub ciągłego, w którym na osi odciętych występuje częstotliwość. Dla wspomnianej już przykładowej funkcji widmo ma postać pokazaną na rysunku 9.1. Jak widać, szereg Fouriera (9.2) pozwala przejść od postaci analitycznej funkcji (lub wykresu) do postaci widmowej. To przejście nazywa się transformacją Fouriera.

Obliczanie współczynników Fouriera

Aby wyznaczyć analitycznie współczynniki Fouriera, dokonujemy pewnych operacji na równaniu (9.2), mianowicie mnożymy obie strony równania przez

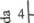
s

u

U

0 co 2(0 2>co 4co 5<o 6co Częstotliwość

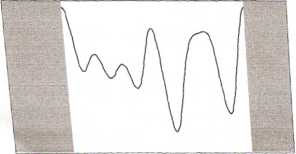
Rys. 9.1. Funkcja złożona z czterech funkcji harmonicznych: j(f) ⁼ 0,9 + 1,2 cos (pot) +

+ 0.3 cos (3<of) + 2,5sin (3a>f) + 3cos (4cot) +2cos (6co/); biały obszar obejmuje pojedynczy okres T, co oznacza częstotliwość kołową (<o = 2ic/1); po prawej widmo fourierowskie funkcji