64 (95)

64 Stanisław Szuba

64 Stanisław Szuba

(9.5c)

Współczynniki Fouriera dla wybranych funkcji Jeżeli znana jest funkcja_/{/)> równania (9.5a—c) pozwalają na obliczenie wartości liczbowych współczynników Fouriera. Rachunki analityczne są łatwe tylko w przypadku prostych funkcji, np. piłokształtnej, prostokątnej czy trójkątnej. W innych przypadkach całkowanie jest trudniejsze; wówczas stosuje się numeryczne obliczanie współczynników za pomocą komputera.

PRZYKŁAD - obliczanie współczynników Fouriera dla funkcji piłokształtnej

Funkcja piłokształtna zmienia się liniowo w ramach pojedynczego okresu, na granicy okresu skokowo wraca do wartości z początku poprzedniego okresu i następnie znowu powtarza przebieg liniowy (rys. 9.2a). W ramach jednego okresu możemy ją wyrazić w postaci równania:    ⁼ kt, gdzie k jest współczynnikiem nachylenia. Do znalezienia

Rys. 9.2. Funkcja piłokształtna a) przebieg matematyczny, b) suma 4 składowych harmonicznych, c) suma 20 składowych

współczynników Fouriera wykorzystamy równania (9.5) i wstawimy do nich aktualną postać funkcji. Równanie współczynników parzystych przyjmie postać:

2

a„ = — T

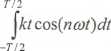
(9.6a)

Można łatwo sprawdzić, że funkcja podcałkowa jest anty symetryczna, tzn. zamiana t na -1 powoduje tylko zmianę znaku, a nie wartości. Całka takiej funkcji jest zerem, a więc wszystkieparzyste współczynniki Fouriera są zerowe'.

a_n = 0 (dla wszystkich ri). Analogicznie, równanie (9.5b) przyjmuje postać:

' Tli

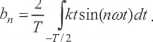
(9.6b)