73 (196)

154_    Przekształcenie Laplace a

UJ l | — Wl    i    |

b) Ponieważ ch tot == ---- oraz £ { e“‘ } = -, £ { e^-1"¹} = - więc wobec

2    '    ’ s — w 'J s + u>

liniowości przekształcenie Laplace’a mamy

£{chwt} = £ | ^eW'±f~. | ^ \ [C { e^w>} + £ { e— }] i’ r_i_ i i _ s

2    — u/^s + u>J s² — oj²

Korzystając z kolei ze wzoru

£{/(<- to) 1 (i - <o)} =e"^i,0£ {/(/)} dla to ^ 0

mamy

£ { ch (ud — or)l(ud — a)} = £ | ch    ^ 1 ^u; (^t — — j-

_ ££    __sa

= e “ £ { chód} = e

s² — w²

c)    W tym przykładzie wykorzystamy fakt o przesunięciu argumentów obrazu, tj. wzór

£ {e^a‘/(0} = ^F(^s ~ “). gdzie £ {/(<)} = ^F(s).

Ponieważ (zobacz przykład a))

r i 2    s² + 2w²

¹    1 s(s² + 4w²)’

więc wobec podanego powyżej wzoru otrzymamy

r I at 2    (s - a)² + 2w²

*•    ‘ (s — a) [(s — a)² + 4ui^J]

d)    Mamy

m = o - «"*) [i(o -1(‘ - t)]+(i - *-^T) i(< - t)

= l(t) - e~'l(0 - 1(4 - T) + e^_'l(f - T) + l(t - T) - e~^Tl(t - T)

= 1 (t) - e~‘l(t) + e~^Te~^(,~^T)l(t - T) - e~^Tl(t - T).

W powyższych przekształceniach dążyliśmy do takiego przedstawienia funkcji f(t), aby można było wykorzystać wzór • (przykład b)). W konsekwencji mamy

r (/(■)) = T - T^T + -«-^r‘-^rT - •

1    1    -r _,r    1    -t -mt]_

s s -f* 1    s+1

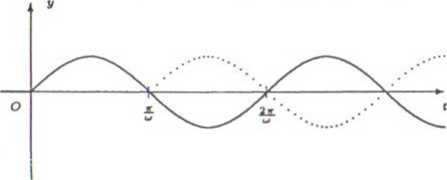
e) Ponieważ funkcję f(l) możemy zapisać w postaci (zobacz rysunek)

s s(s + l)

/(<) = sin uit •!(<) + sin w (t — — j • 1    — — 'j ,

Jedenasty tydiie* - odpowiedzi i wskazówki ;;l “' L . J    ,    155

więc wykorzystując wzór • z przykładu b) otrzymujemy

£{/(<)} =

S² + Ul²

s² + Ul²

=    1 + e

SIT \

Ul \    Ul

I S² + UI²

Zadania

O Zadanie 11.1

Narysować wykres funkcji /(<) i znaleźć jej transformatę Laplace’a, jeżeli:

’ 1 dla t G (0,1), -1 dla t € (1,2), 0 poza tym.

0 dla t < 0,

a) f(t) = t dla te [0,1], b) /(<) =

1 dla t > 1;

O Zadanie 11.2    ,

Niech £ {/(Ol ⁼ F(^s)- Udowodnić następujące własności przekształcenia Łapiącej i przekształcenia odwrotnego: a) £ {e^atf(t)} = F(s - a), gdzie a G C;

b)    £ {/(a<)} = -F (-), gdzie a > 0;

a \a/

c)    £^_1 {F(cs)} = -f , gdzie c > 0.

O Zadanie 11.3

Korzystając z własności przekształcenia Laplace’a wyznaczyć transformaty podanych funkcji:

a) f(t) — sh u>t\

b) /(<) = sin²ud;

c) f(t) = cos (ut — ć) l(w< — 6); d) /(<) = e^at sin² cjt\

0    dla    t < 0,

t    dla    t € [0,1],    f) /(O =

1    dla    Ol;

e) f(t) = <

Odpowiedzi i wskazówki

11.1 a) 11.3 a)

1 — c”

-;b)

— 3    ,    —23

1 - 2e~‘ + e

1 dla t G (0,1), -1 dla t G (1,2), 0 poza tym.

^e)

1 -t

-;f)

²’"' 2s 2(s²+4w²) 1 - 2e~* + e^-2*

4² + w² ’    2(a — a) 2 ((j — a)² + 4u>²] ’

s