75 (112)

(manipulacyjnych; myślowych i symbolicznych działaniowych) prowadzących do rozwiązania problemu matematycznego lub tylko uzyskaniu] odpowiedzi na pytanie zawarte w zadaniu. Początkiem rozwiązania zadania tekstowego jest uchwycenie danych oraz związków i zależności między] nimi a głównym pytaniem.

Program mówi o metodach arytmetycznych i algebraicznych ro/wią-J zywania zadań. Myślę jednak, że należy rozumieć lo bardzo szeroko, od| wszelkich odmian działań konkretnych (łącznie / operowaniem pojęciami geometrycznymi) poprzez czynności wyobrażane częściowo werbalne (umowne), aż do działań abstrakcyjnych (symbolicznych).

W trakcie tych czynności mamy do czynienia z trzema typami] sytuacji związanych / rozwiązywaniem zadań tekstowych, mianowicie:

U Rozwiązywanie zadań tekstowych pod kierunkiem nauczyciela.

2.    Rozwiązywanie zadań tekstowych analogicznych, nieco modyfikoi wanych, z nieznaczną ingerencją nauczyciela.

3.    Rozwiązywanie samodzielne zadań tekstowych.

Chciałbym obecnie, na przykładzie dwóch zadań, pokazać różne sposo-j

by rozwiązań, które można stosować w klasie 1. Rozwiązanie zadaniu wieloma sposobami jest korzystniejsze niż rozwiązanie w tym czasie dwóch] czy więcej różnych zadań. Uczeń pozornie tylko rozwiązał jedno zadanie! ale w tym jednym zadaniu zauważył dużo zależności i związków oraz ich] interpretacji. Takie działania przygotowują ucznia do późniejszego rozwiąż zywania wielu zadań w znacznie szybszym tempie niż to jest zazwyczaj,j Zadanie 1

Ala znalazła kilka borowików, a Adam 3 rydze. Razem dzieci znalazł}

9 grzybów. Czy umiesz obliczyć różnymi sposobami, ile borowików znała/.-] ła Ala?

1.    Rozwiązanie manipulacyjne (inscenizowane) na konkretach (wycie] tych grzybach-żelotiach). Układanie 3 rydzów i tylu borowików, żeb} było razem 9 grzybów. Przeliczenie borowików (6) jako rozwiązańilf zadania.

2.    Rozwiązanie za pomocą rysunku konkretnego. Podobnie jak poprzedj nio, ale uczniowie rysują rydze i potem tyle borowików, żeby razenj było 9. Następnie przeliczają borowiki.

3.    Rozwiązanie za pomocą liczmanów. Ułożenie 9 liczmanów białych (grzybów). Ułożenie pod nimi 3 rydzów (liczmanów pomarańczowych)] a pod pozostałymi borowików (liczmanów brązowych) i przeliczenie (6)J

4.    Rozwiązanie na zbiorach za pomocą pętli. Narysowanie w pętli ⁽1 kroi pek (grzybów), utworzenie podzbioru rydzów (3 kropek), a następnie utworznie drugiego podzbioru z postałych kropek (6) i przeliczenie go. Próba napisania działania.

5. Rozwiązanie na schemacie prostokątnym (przygotowanie do równania). Uczniowie rysują 9 okienek (liczba grzybów). W ostatnich 3 rysują rydze, a w pozostałych borowiki (6). Borowiki oznaczają klamrą i piszą niewiadomą x. Po przeliczeniu równa się 6.

(>. Rozwiązanie na kolorowych liczbach. Uczniowie pod klockiem 9 układają od końca klocek 3, a następnie dopasowują klocek 6 i odczytują rozwiązanie. Mogą to też narysować.

7. Rozwiązanie na grafie liczbowym i grafie do równania

+ 3    +3

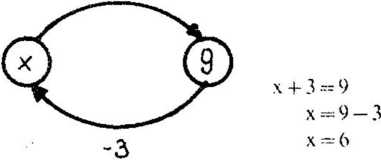
O

-3

8. Rozwiązanie na osi liczbowej. Uczniowie zaznaczają na osi liczbowej 9 odległości i odliczają 3 w kierunku zera. Pozostałe 6 odległości zaznaczone strzałką w kierunku zera jest rozwiązaniem zadania.

- X

x + 3 = 9 x — 9 — 3 x — 6

9.    Rozwiązanie na drzewku.

10.    Rozwiązanie określane słownie i zapisem formuły matematycznej. Zadanie 2

Janek kupił bilet autobusowy za 9 z.l i zeszyt. Do kasy dał 20 zł i otrzyiąał S zi reszty. Ile kosztował zeszyt?

I. Rozwiązanie zadania na konkretach. Uczniowie układają 20 krążkóW. a pod spodem bilet i zeszyt. Dziewięć krążków układają pr/y bilecie plącąc za niego, a następnie 5 krążków odsuwają jaku iwie i pozostałe krążki zostają pr/y zeszycie, obrazując koszt /es/uu (ó).

147