CCF20091014019 (2)

inośc odkształcenia odpowiadającego sile P, możemy sporządzić TKyfcę ż = f(P) oraz wyznaczyć stałą sprężyny (rys. 11.3):

P — CA, C = tg fi,

P

Gd⁴ N

c = — A

$D³n mm

(11.5)

c aos nazwę sztywności sprężyny lub stałej sprężyny i jest liczbowo 'ozciągającej łub ściskającej sprężynę, wywołującej jednost-inrę jej długości.

11.2. CEL ĆWICZENIA

-TBTCZi:;;a jest:

■y n-nz-er e skrócenia /. układu dwóch sprężyn o jednakowej wysokości, rsn:    srcćegle i ściskanych siłą P;

r-r.— -.-rz- e wartości sił ściskających każdą ze sprężyn, ipsEKzemc mcdulu sprężystości postaciowej G materiału sprężyn. gj- zrda dla których przeprowadzono obliczenia szczegółowe, BBC n rys. 11.4.

■i—r zstizdu złożonego z dwóch, sprężyn (rys. 11.4) pod wpływem i- F - reślimy doświadczalnie. Po wyznaczeniu skrócenia /, ~ redzie możną przystąpić do określenia wartości sił ściskających BBce ścrarry. Przyjęto następujące oznaczenia:

—    sin SvTi*:^;ąca sprężynę zewnętrzną,

—    saską) ąca sprężynę wewnętrzną,

—    s-ecr 'i r działowa sprężyny zewnętrznej,

—    eedmei podziałowa sprężyny wewnętrznej,

Łi**crcr. drutu sprężyny zewnętrznej,

ca zrutu sprężyny wewnętrznej, r. r sprężyny zewnętrznej, r* r ow wewnętrznych,

^srężystości postaciowej sprężyny zewnętrznej, Łrężystości postaciowej sprężyny wewnętrznej, err* ach odkształcenia obu sprężyn można wyrazić w postaci:

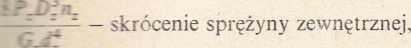
ii

— - skrócenie sprężyny wewnętrznej.

163