CCF20081211005

440 Rozwiązania i odpowiedzi

440 Rozwiązania i odpowiedzi

(1__LJj

\a² sin² a/

6.102. a^O, sina^O, z' = (acosa — sina)

,    _    , (l+tgx)(sinx + xcosx) — xsinxsec² x

6.103. tgx*-l, y'=-TT——72-

(i +tgxr

, sinx+cos x + x(sin x — cos x)

1 +sin 2x

6.104.    sin2x7>t — 1, y = -

6.105. / = — sin³ x.

6.106. y' = sin²xcos⁵x

,    2 sin³ Jx ^    —3

6.107. x^0, cosJxJ=0, y =—-t—— . 6.108. sinx^0, y' =—_z—

y/xcos^sJx    sin x

6.109. y'=(a +l)e^0Xsinx.

6.110. y = xe^2x(2 sin x + xcosx + 2xsinx).

2Xy/x

6.111. x>0, y

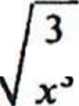
6.112. x>0, y'= — 3 ./— sin" _ / — cos

, 7sin³x

6.113. cosx^0, y =-₅—

cos x

COS X

6.114. sinx^0,    3-7-7—(2+cos² x).

sin x

6.115. x>0, sinx^0, y'

1

2 Jsinx+yjx+2y/ 6.116. x^0, cos^x+-^-^0, tg^x+-^>—1 »

:

cosx +

I(_l+n}.

yjx+2y/x\ yJ^x) J

x²-l

/ =

2x

6.117. cos 3u 5*0, z' =

*

3

cos² 3u

6.119. y' = 4cos4x.

6.118. z' = tg²u+ctg²u.

3

6.120. / =

1 +9x'

6.121. y' =

14

4+x

2 •

6.122. 0<f<2, x' =

-1

V«(2-r)

6.123. —l<r<l, x' =

6.125. |tl> 1, x' —

|r|vW

-1

6.124. 0<K1, x' =

|.|V«²-i

6.126. y'=0. Uwaga. W przedziale 0<x< 1 zachodzą następujące równości

arcsin V1 — x² - arccos x i arcsin x+arccos x = lu_t a więc w tym przedziale funkcja y jest stała: y=łn.

6.127. —1<<<1, x'

6.128. y' =

1

2(x²+l)

6.129. x> 1 , / =

xlnx

V(*²- l)² ’

6.130. y'= arctg x.

6.131. y = x⁴ arctg x +

x⁵ — x

6.133. — l<x<l,y' =

5(1 4-x²)    ⁵

____V?_

(l+x²)Vl-x²’

+ jx³-!x. 6.132. y' =

1

1 +x

6.134. — l<x<l,y' =

-1

2 V(l —x)(l+x)

6.135. y = —.

l+x²

6.136. y' =

1

2 (1 +x²) *

6.137. y' =

1

2\ *

2 (1 +x )

6.138. arcctg 2x^0,    y^ł =

71

(1 +4x²) (arcctg 2x)‘

6.139. arcsin y^± 1, z' =

1_ li

csin v\² — 11 V 1

— arcsin y

6.140. y' = 3x² arctg³ x +

Vl — y ² [(arcsin y)² — 1] ^ ¹ + arcsin y 3x⁵

l+x⁶ ‘

6.141. y# ±i,

(1 — 4y)²

6.142. y' = —

sin x 2+sin x

6.144. y' = 3e^3x.

6.146. y'=e*(/(x)+/'(x». 6.148. y'=e*^{,n x} cos x. 6.150. y'= — e^co*² * sin 2x.

G/bS^+arcs“^4y) •

6.143. y=--—— -.

a+b cosx

6.145. y' = |e^łx.

6.147. y'=3e^-2x(—2g(x)+g(x)). 6.149. y^#=-5e^co*^xsinx.

6.151. y^/ = 18e²*^I“^Sxsin² xcosx.