CCF20120509024

no i. ri/.YKiuuy i /.auama

5.5.4. (Rys. 1-5.40). Podczas projektowania kanału o przekroju poprzecznym w kształcie trapezu równoramiennego, przyjęto pole powierzchni przekroju przepływowego równe A oraz wysokość zwierciadła cieczy nad dnem h. Wyznaczyć kąt a nachylenia ramion trapezu, przy którym natężenie przepływającej cieczy będzie największe. W celu rozwiązania zadania, skorzystać z definicji promienia hydraulicznego.

5.5.5. (Rys. 1-5.41). Do wyznaczenia współczynnika lepkości kinematycznej nafty, użyto rurki o średnicy wewnętrznej d = 10 mm i długości / = 3 m. Rurkę podłączono poziomo do otwartego zbiornika, w którym utrzymywano stałą wysokość zwierciadła nafty h = 0,4 m oraz stałą temperaturę. Określić współczynnik lepkości kinematycznej nafty w danej temperaturze, jeżeli w ciągu jednej minuty przepływało przez rurkę ruchem ustalonym 2,52-10”³ m³ cieczy.

	V
			i
	—	t)
		£-

Rys. 1-5.41

\k

5.5.6. Przez przewód o średnicy d przepływa ruchem laminarnym ciecz o gęstości p. Zakładając, że spadek hydrauliczny wynosi J, wyznaczyć naprężenia styczne x_a, występujące na wewnętrznej ściance przewodu.

5.5.7. (Rys. 1-5.42). Z zamkniętego zbiornika instalacji hydroforowej wypływa woda przewodem o zmiennej średnicy. Temperatura wody T = 286 K. Jakie ciśnienie powinna wytwarzać pompa zasilająca zbiornik, aby objętościowe natężenie przepływu wody w rurociągu wynosiło 4■ 10~³ m³-s^_1. Wymiary poszczególnych odcinków rurociągu wynoszą: d_x = 80 mm, l_x = 200 m, d₂ = 50 mm, l₂ = 100 m, a ich chropowatości bezwzględne: k_x = 0,67 mm, k₂ = 0,2 mm.

Uwaga: Właściwości wody oraz współczynniki strat wyznaczyć na podstawie tablic pomocniczych i wykresów.

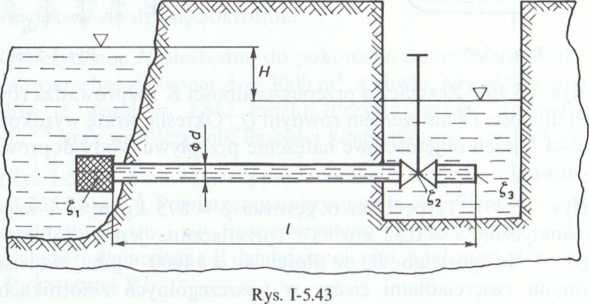
5.5.8. (Rys. 1-5.43). Przewód o długości / = 500 m i chropowatości bezwzględn k = 0,72 mm ma doprowadzić wodę z rzeki do zbiornika wyrównawczego, zasilającej stację filtrów o wydajności Q = 180 m³/h. W okresie najniższych stanów woc zwierciadło rzeki znajduje się na wysokości H = 6 m ponad zwierciadłem wody zbiorniku. Stosując metodę iteracji, obliczyć średnicę d przewodu łączącej rzekę ze zbiornikiem wyrównawczym wiedząc, że współczynniki strat lokalny! dla kosza ssącego, zaworu zasuwowego oraz na dopływie wynoszą: £, = 7, £₂ = 0, £₃ = 1. Przyjąć temperaturę wody T = 278 K oraz średnią prędkość przepływ c = 2 m-s^-1. (Zalecana prędkość przepływu w instalacjach wodociągowy! 1 m-s^_1^c<3m-s^_1). Pozostałe wielkości, niezbędne do rozwiązania zadań odczytać z tablic pomocniczych i wykresów.

5.5.9. (Rys. 1-5.44). Zbiornik ciśnieniowy A i otwarty B połączono przewodei składającym się z trzech odcinków połączonych szeregowo, których długości wynosz l_v l₂ i /₃, a średnice: d_x, d₂ i d₃. Nadciśnienie w zbiorniku A jest równe p, a różnii poziomów zwierciadeł cieczy w obu zbiornikach — H. Pomijając straty lokalne on zakładając, że współczynniki strat liniowych dla kolejnych odcinków rurociąg wynoszą odpowiednio:    X₂ i ż₃, obliczyć objętościowe natężenie przepływu ciecz

Przyjąć ciężar właściwy cieczy wypełniającej zbiorniki równy y.