3784493655

Praca Doktorska - Anna Sapińska- Wcisło

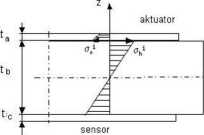
Rys 2.8 Schemat rozkład naprężeń dla przekroju poprzecznego aktywowanej belki.

Zaniedbując naprężenia występujące w sensorze i przemieszczenie osi obojętnej, po całkowaniu momentu równowagi względem osi obojętnej, otrzymamy zależność pomiędzy naprężeniami powierzchniowymi dla belki i aktuatora.

g[ = -Ka^la    2.18

gdzie:

_K_ 3 y

t\ + — (3 t_bt²a +4t])

^Eb

2 E_hJ_h

Odnosząc się do zależności określającej moment gnący M_a =—-——s'_b, stała aktuatora może być określona jako

2.19

KE_aE_bt²bd_n

^a 6 t_a(E_b+KE_a)

Zakładając, że sensor i aktuator połączone są za pomocą układu ze sprzężeniem zwrotnym, napięcie przyłożone na aktuator jest określone zależnością

dV

V = kV +k_d—ł    2.20

'    Bl

gdzie: k_p i k_d są odpowiednio proporcjonalnym i różniczkującym współczynnikiem wzmocnienia.

Po podstawieniu równania 2.21 i 2.7 do równania 2.8 otrzymamy następującą zależność definiująca moment gnący:

M„(xt) = C.CA (x)(k + kj ^-) f    (x)dx    2.21

dt ^J0 dx

Efektywna powierzchnia elektrod aktuatora i sensora została doprowadzana do postaci:

15