3784493654

Praca Doktorska - Anna Sapińska- Wcisło

2.13

E_aE_ht_h(t_h +t_a)d_3i 2(E_bt, + E_at_a)

Omówienie drugiego z pojęć, dotyczącego określenia wartości momentu gnącego generowanego przez aktuator jest równoznaczne z faktem, że w przypadku tym rozważyć należy nie tylko wydłużenie aktuatora, ale także jego ugięcie. Analiza zagadnienia została przeprowadzona przez Crawleya i Luisa (1987), a następnie Dimitriadisa (1991), którzy przy użyciu klasycznego rozkładu naprężeń dla przekroju poprzecznego układu belka- aktuator uzyskali zależności:

dla belki    <r_b = 2a'_b —    2.14

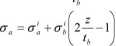
2.15

dla aktuatora

gdzie:

<j'_b,c'_a -przedstawiają odpowiednio naprężenia belkę i aktuator, z- odległość powierzchni styku od osi obojętnej

Porównanie momentów aktuatora uzyskanych bazując na klasycznym rozkładzie naprężeń [55,20] (wersja nr.3, uprzednio rozpatrywanego modelu, w której E_s = 0, d₀ = 0), wskazują, że obliczone wartości stałej C_a ulega różnym zmianom, w zależności od modelu, wraz ze wzrostem stosunku szerokości układu aktuator/belka. Aktuator zginany z naprężeniem opisanym identycznie jak w przypadku belki, zadziałałby ze znacznie pomniejszonym efektem aktuacji. A zatem, zmiana rozkładu naprężeń będzie konieczna, jako że parametry sztywności , odpowiednio dla materiałów piezoelektrycznych i struktur stalowych znacznie E    E

różnią się od siebie (dla ceramików PZT--- » 0,25, dla polimerów PVDF--- » 0,01).

E_b    E_b

Zmodyfikowany rozkład naprężeń jest wyznaczony przy założeniu jednakowej liniowej zmiany odkształcenia zarówno dla belki jak i aktuatora. W tym przypadku naprężenie dla aktuatora zostanie uzyskane przez zastosowanie prawa Hooka, wraz z uwzględnieniem modułów Younga aktuatora, oraz belki.

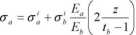
2.16

Powierzchniowe naprężenie aktuatora <r'_a jest powiązane z elektrycznie indukowanym wolnym odkształceniem A oraz powierzchniowym odkształceniem belki s‘_b zgodnie z poniższą zależnością

2.17

cr'_a =E_a(s_b - A)

Rozkład naprężeń, dla przekroju poprzecznego aktywowanej belki, zdefiniowany przez równanie 2.17 i 2.18 przedstawia rysunek 2.8.

14