CCF20120509079

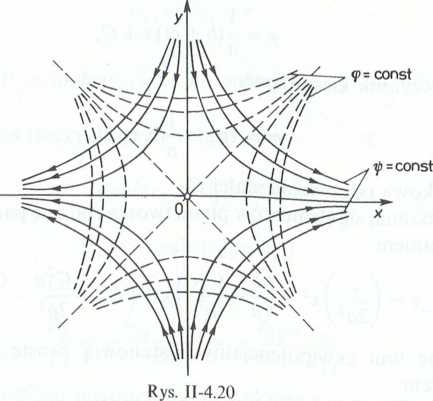
4.5.7. a. Linie prądu są hiperbolami opisanymi równaniem:

ij/(x, y) = axy = const,

których asymptoty pokrywają się z osiami układu współrzędnych (rys. 11-4.20). Linie ekwipotencjalne również stanowią rodzinę hiperbol, spełniających równanie:

<p(x, y) = \a(x² - y²) = const.

b. Składowe wektora prędkości wynoszą:

v_x = ax oraz v_y = ~ _ay,

a jego moduł

|v| = dy/x² + y².

4.5.8. Funkcję prądu, przedstawioną graficznie na rysunku II-4.21 a i b opisuje następująca zależność:

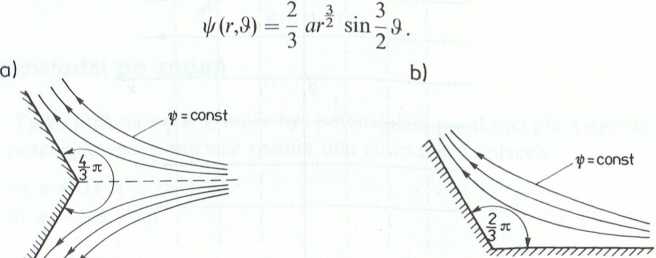
Rys. 11-4.21

Składowe wektora prędkości wynoszą:

i . 9 — ar² sm —, 2

i 9

v_x = ar² cos - oraz v_y =

a jego moduł

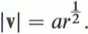
4.5.9. Funkcja prądu:

<A(x, y) = y ln Jx² + y² + xarctg

a potencjał zespolony:

w(z) = z lnz.

4.5.10.    a. Przepływ jest wirowy, o strumieniu wirowości co = —2a. b. Przepływ jest niewirowy, a zatem a> = 0.

4.5.11.    Cyrkulacja prędkości F = —2nd².

4.5.12.    Równanie linii prądu:

QS

r = Ce^r,

opisuje rodzinę spiral logarytmicznych przedstawionych na rys. II-4.22.

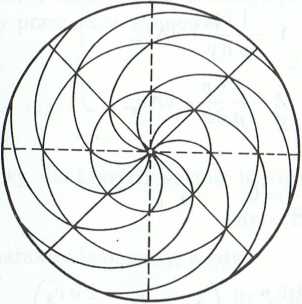
Rys. II-4.22

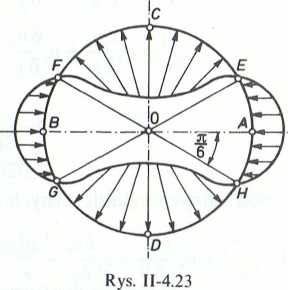
4.5.13. Rozkład ciśnień na obwodzie walca (rys. II-4.23) opisuje równanie:

P = Po+~v²(\ —4sin²9).

₄ = 0 ti/2). oraz

Ciśnienie osiąga wartość maksymalną p = p₀ + pv²/2 w punktach A i B (9, i 9„ = Ti), a minimalną p = p₀ — ?>pv²/2, w punktach C i D (9_C = ti/2, 9_d =

W punktach E, F, G i H, określonych kątami: 9_£ = n/6, 9_F = 5ti/6, 9_c = 7tc/6 IIn    11 n/6, ciśnienie p = p».

' Mo li,mik.i dKhou