CCF20120509056

Lzęst 11. ito/.wiązama i oupowicazi

W ruchu ustalonym linie prądu pokrywają się z torami cząstek płynu. Równanie toru elementu płynu otrzymamy po rozważeniu jego przemieszczenia w elementarnym czasie dt, a wówczas

dx = i^dt, dy - v_ydt;

stąd

(6)

dx dy

»x ^vy

gdzie

v_x = v_x(x, y, t) oraz v_y = v_y{x, y, t).

Jeżeli analizowany przepływ jest potencjalny, czyli niewirowy, to

0X

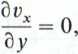
(7)

a zatem istnieje taki potencjał prędkości (p, dla którego

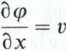
d(p

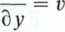
y’

(8)

przeto

dę =

—dx + —dy.

ox cy

(9)

Po podstawieniu wyrażeń (8) do równania ciągłości (1), a wzorów (3) do warunku potencjalności (7) otrzymamy:

(10)

(U)

9²<p d²(p 9x^{2 +} 0y²

oraz

0²i\i 0²ih 0x^{2 +} 0y²

skąd wynika, że funkcja prądu i potencjał prędkości ę spełniają równanie Laplace’a, a zatem są harmoniczne.

Objętościowe natężenie przypływu przez prostokąt elementarny dni, tj. dla warstwy o grubości jednostkowej, wynosi:

di1/

dQ = ——dn = di/i. dn

Wobec powyższego, objętościowe jednostkowe natężenie przepływu między powierz chniami prądu if/₁ i ij/₂ jest równe:

^2

Gi,2 = J d«A =    (12

«/m

Zgodnie z warunkami Cauchy’ego-Riemanna,

ę(x,y) + 'up(x,y)

jest holomorficzną funkcją zmiennej zespolonej

z = x + iy.

Funkcję

w(z) = (p(x, y) +ii//(x, y)    (13

nazywamy potencjałem zespolonym, którego pochodna

Ponieważ

dw 8 (p .dii/    ,d(p 8i1/

dz    ox dx 8y 8y

(\A

8 ij/    dę

- = _Vx oraz - = v„

zatem prędkość zespolona

(15

dw

^v = - = _Vx-_lVy,

a jej moduł

» = y/v* + vj.

Jeżeli r i .9 są współrzędnymi układu biegunowego, to

v_r = v_xcos 9 + ^sin 9,

v₉ — — v_xsin9 + v_ycos9    (16

i można wykazać, że

dw iS

ćb^C

przy czym

z = x + iy = re^lS = r(cos9 + i sin ĆJ), r = y/x² + y².

(17