CCF20130109032

4. STAN NAPRĘŻENIA I ODKSZTAŁCENIA. PRAWO HOOKE’A

4.1. DEFINICJA NAPRĘŻENIA

Rozpatrzmy ciało obciążone układem sił zewnętrznych będących w równowadze. Dokonajmy myślowego przekroju tego ciała dowolną płaszczyzną, jak pokazano na rysunku 4. la. Każdemu punktowi leżącemu na płaszczyźnie przekroju jest przyporządkowana siła wewnętrzna, przy czym układ sił zewnętrznych i wewnętrznych działających na obie części ciała pozostaje w równowadze.

a)

b)

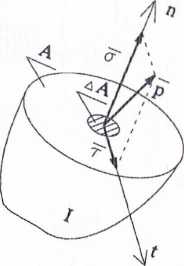
Odrzućmy myślowo część II ciała. Wydzielmy na płaszczyźnie przekroju wokół obranego punktu K element powierzchni AA. Niech AP oznacza sumę sił we-

AP

wnętrznych, przyporządkowanych powierzchni AA. Iloraz -jest średnią gęsto-

AA

ścią sił wewnętrznych na powierzchni AA. Gęstość sił wewnętrznych w punkcie K

AP    -

będzie granicą ilorazu - przy AA—>0. Granicę tę oznaczamy symbolem p

AA

i nazywamy wektorem naprężenia w punkcie K

W praktyce nie korzysta się z definicji naprężenia opisanego wzorem (4.1), lecz wprowadza się pojęcie naprężenia normalnego a i stycznego T, przy czym

]} = a+f.    (4.2)

Wymiarem naprężenia jest N/m². Jednostkę tę nazywamy paskalem i oznaczamy symbolem Pa. Do celów technicznych stosuje się jednostkę o wartości 10⁶Pa = I MPa (megapaskal).

4.2. POJĘCIE STANU NAPRĘŻENIA W PUNKCIE.

NAPRĘŻENIA GŁÓWNE

Naprężenie w punkcie przekroju zależy od orientacji przekroju, a także od położenia punktu, w którym to naprężenie badamy.

Ponieważ przez dany punkt możemy poprowadzić nieskończenie wiele płaszczyzn, w punkcie mamy nieskończenie wiele wektorów naprężenia. Do opisu stanu naprężenia w punkcie wystarczy znajomość naprężeń w trzech wzajemnych pro-.(opadłych przekrojach.

Poprowadźmy przez wybrany punkt K trzy przekroje prostopadłe do osi przy-lęlogo układu współrzędnych. Otrzymujemy trzy wektory o współrzędnych pokazanych na rysunku 4.2.

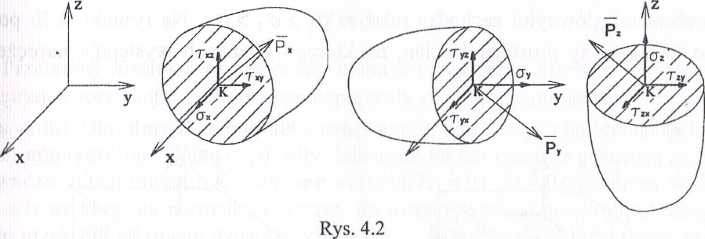
Wektory te są liniowo niezależne. Opisują stan naprężenia w danym punkcie K.

	Px			^TXV	Gz
Pk =	El	=	yx	°y
	Pz	K	y*	^zy	<r,_

Stan naprężenia w danym punkcie ciała jest zatem określony przez dziewięć składowych: trzy naprężenia normalne i sześć naprężeń stycznych.

61