CCF20120622�010

O-CSl -n*
o
— 5i-nX \m/K - sin oC
- CMCXH (.XX* 1 = X •X. <
liM/k^jO^ cjOTK^j' <^AvXvut^ CuX'‘^OX'U vU(1a. 'J^j- . Fun/kCj.^ C^orn^j' l^KX^\jLC^j UXl \ix2uXKvuCX '•RA*V kc//c\ po^hau
(X'efx ,

k_<yA. ^ n/ć}.2<
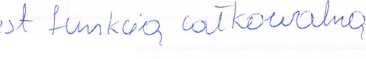
<T / d
\/S £cx,łs] . Kp CX/(jJ
-F-6- jdnicLS^\ ^MXoimClXnxij xG^ p't~zŁÓZ^QjU? (ĆX/(rJ
sj
cn
ur [a, Lr] ,
2 _ p(Vj po^COjio^ pocJwdnjĄ l F(pj - fU) pjax h^ok yi dio. kJjjy^cA lu) je& ji^yJiCj'-^ U-OjC^lą .
(fJ~^ *- 2 ćMChn* j ■
u
tX

4- -!
i f-x‘
(r
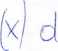
M d/
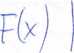
Ir
a
^ lir
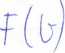
O
Lr
J
cx
X
dF
_ x
-2 2 -a y
<e
,/uT. KI^iaJTD^k^
KKeod

xa
d „
_J b^dzre ol^ąIcv ur pl.'^d^odfe [a ;dj i/ nOecA
(£ (x) b^d^e funkio) pieyuroŁhCj j^ijF f(x) <s®Stetóu UJkAj^
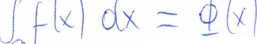
Wyszukiwarka
Podobne podstrony:
kola semestr 1 KOLOKWIUM (Ml) Zad. 1 Oblicz f—— -dx J x* - 4x Zad.2 Oblicz 1 sin" x Zad.3 Badaj
CCF20100119�020 -i-B.51 nZtT-^r2 + 6iJk V IV + Bk1 sin wt M. v WT1 + Bfc» 1FB TT r .4.n- k t TCOS
CCF20120622�009 x x oonsh, ■0 dx - -txa l-ur- o iAXvte>S(x oiia, cxxU<u. ^
CCF20120702�113 a y/Ł- (ói /YZ- CS&tyzyUsp > < C^>ź>VL£j Zć-L.cl
CCF20110105�011 (3) cm/ N V( LA ^ ~ o( a- C0 L£> a~J ^oC m C0 . aiacsq^ ^ ^/u7"r v ^sa/~ L
CCF20110524�007 obi^crłosiO -^ ę>QjfZxDcyk/~iom3m© ~ ^ pTO-c^^p.° cu&kTćp oc^y C^€/SvK^StxjfO
Wydłużenie próbki (4)o wielkość Al spowoduje obrót pryzmy (3) o kąt oC frys. 2.4), więc Al =» b sin
DSC02449 (2) 394 VI. OAa mcozntczons S&dtoswsaiijy 5r*ik 5i!r*4k, zuob j oc*Sxrfx*j Jcos» du «
3 (2796) : I i fi © 7 Korrnf 4©KsC^KJ., •--* -^CcCO*.’ Q rfn^/nx?c^cc-+c><^o . O^/^oc ^. a 4-
Image1827 x = 2arctgf, dx = 2 dt 2 sin sinx =- • 2 x sin — 2 x cos — 2 cos cosx = 2 2 X cos — 2
Image3306 / 1 V 1 V jdy J(2x-y + 1)dx = J J(2x-y + o y2 o[y2 y yz + y° ą. _ 1
img022 FUNKCJA PIERWOTNA, CAŁKA NIEOZNACZONA
img090 WYKAZ WAŻNIEJSZYCH CAŁEK143 </sin*+ecos*+/ 1 f asi ’ J asi dx = —z-r (ad
dy = (sin(L) • sin(^) • cos(As) - cos(Z) • sin(/lj ))• (dX - dXs)... + (sin(£) • sin(^ę) • sin(A,) +
więcej podobnych podstron