DSC00069 (2)

byłaby wtedy dwusieczną kąta zewnętrznego. kąta jest zatem punkt N. Niech to będzie wierzchołek B I

układ równań

3x+y-3=0.    x~»’-t-S=0

znajdujemy, ie B(-\, f). Znajdźmy punkt symetryczny do punktu j! względem dwusiecznej x-> + 5=0. (por. zad. 287). Punkt ten 4 Ttzeci bok przechodzi przez punkty A, i B i ma równanie x+3v~I3*o

320.    (f, -|).

321.    Znajdujemy równania dwusiecznych dwóch kątów, a następni; punkt ich przecięcia (—2, —0).

322.    Bok BC tworzy z dwusieczną kąt, którego tangens jest rów* r+2=y. Taki sam kąt tworzy dana dwusieczna (rys. 76) z bokiem dC. Bok AC ma równanie y—m\. Współczynnik m znajdujemy 1 waruaks

ł —tu 1

.    — —..... ne —

1 *-m 3 '

skąd m=i. Zatem bok AC ma równanie y*jX. Punkt C znajdujemy z układu

x-2>=0, x—y—4=0:

C(8,4). Mając punkt C i wektor BC, znajdujemy B(3, -6). Równania boków AB i BC są odpowiednio 2x+y=0, 2x— y—12=0.

323. AC: 5x+12„v+16=0, BO. 3x-4y+24=0.

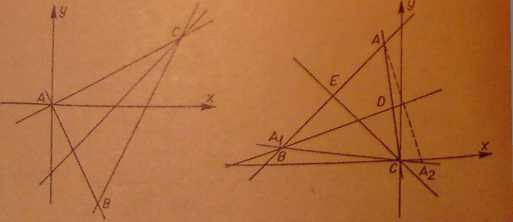
314. Znajdujemy punkty A, i Ai symetryczne do pmtlaA **0gim ' dwusiecznych CE i BD (por. zad. 237). Punkty te (ryt. 77) Mjąynpg, rzędne /<,(- 7,1), X_a(|, - i). Przez te punkty przechodzi Ml WC+tfc-A naniu jc+7y >» 0. Wierzchołek B znajdujemy I okładu

x-3y+10-Ó,    x+7y»0,

a wierzchołek C z układu

X + 7ya>0, X + y—0. S .

Stąd otrzymujemy 5(—7,1), C(0,0). Prowadząc proete przez punkty a i B oraz A i C znajdujemy równania boków

AB: x-y+8»0, AC: 7x+y«0.

325.    Nie. Nie istnieje takie A, dla którego otrzymamy prostą Aix+

326.    Równanie pąku prostych przechodzących przez ponkt przecięcia danych ma postać (por. (3.4.9) i (3.4.10), S 39),

(1)    3x+4y—5+A(2x+y-3)=*0-

Z pęku tego mamy wybrać tą prostą, która przechodzi przez dany punkt Wstawiając współrzędne danego punktu otrzymujemy 2-A’O-O. Zatem równanie (ł) nie obejmuje szukanej prostej, którą jest 2x+y-3=»Q,

327.    Piszemy równanie pęku prostych 2x+y-8+A(x-3y+4)*=Q. Wstawiając tu x=y=0 otrzymujemy —8+4A=»0, tzn. A=2. Równam stukanej prostej ma więc postać 4x—5y=0.

328.    Z pęku prostych 2x—7y—8+A(3x+2y+5)*0 wybieramy prostą spełniającą warunek

2+3A -7+2*

2    3    '

Z warunku tego otrzymujemy A= -4, tzn. szukana prosta ma równam 10x+15y+28=0,

329.    17x+i7y-10=0.

330.    2x+>-6=0, 9x+2y+18=0.

333.    3x-y+ł=0.

334.    Środek odcinka AB ma współrzędne (2, —% muszą spełniać równanie 2x+y—2.+X(x-5y-2fy*B. h otrzymujemy, ie A=>|, tzn. szukaną prostą jest fMh

335.    4.v-5.c + 22=0, 4x+y-18=0, 2*-y+l«fc

m

U CWowikł, Pluciński — Za<łanJ#