DSC00879 (5)

154 Estymacja punktowa i przedziałowa

co jest równoznaczne z obniżeniem się estymatora odchylenia standardowego z wartości 0,59 do 0,48).

Nie zawsze musi tak być. Może się zdarzyć, że dodatkowo wykonane pomiary charakteryzują się rozrzutem znacznie przekraczającym ten, jaki się pojawił w próbie wstępnej, a w związku z tym korzystne zmiany wartości n \ t_a mogą nie wystarczyć na zrekompensowanie wzrostu wartości estymatora odchylenia standardowego, co nieuchronnie prowadzi do uzyskania szerszego przedziału ufności, niż zakładano. W tej sytuacji pozostaje jedynie przeanalizować, czy warunki, w jakich wykonywano dodatkowe pomiary, były takie same jak w chwili wykonywania próby wstępnej. Być może uda się tą drogą ustalić przyczynę, która doprowadziła do niewspółmiernego zwiększenia rozrzutu wyników pomiarów dodatkowych. W takim przypadku, po usunięciu tej przyczyny, należy podjąć próbę ponownego wykonania pomiarów dodatkowych w nadziei, że tym razem wszystko odbędzie się zgodnie z oczekiwaniami.

Przedział ufności dla frakcji

Ponieważ końcowym efektem obliczeń ma być przedział ufności dla frakcji, zatem niezbędne się staje poczynienie założenia o tym, że rozkład badanej w populacji cechy jest rozkładem dwupunktowym z parametrem f. Nietrudno stwierdzić, że połowa szerokości przedziału ufności dla frakcji d, co wynika ze wzoru (4.33), wynosi:

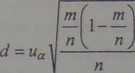
(4.36)

Stosunek m/n jest estymatorem parametru f zatem zakładając jego wartość oraz przyjmując z góry szerokość, a w zasadzie połowę szerokości docelowego przedziału ufności d, można obliczyć liczebność próby n stosując wzór:

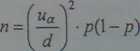
(4.37)

gdzie ni jest oczywiście wartością odczytaną z tablic rozkładu normalnego standaryzowanego przy założonej z góry wartości poziomu ufności 1-a.