DSC03332 (3)

102

niu modeli V_&f v_b oraz predykatu P_Q . Przykład wykorzysta-nia zasady charakteryzacji pokazano w paragrafie 5»5»®* 3>?«2. Przostczeń wartości cech

Wychodząc od cybernetycznego modelu zasobu /3.2.6/, dla każ-dej cechy /kanału/* można określić - na podstawie repertuaru jej | wartości — przestrzeń wartości cechy 0^ opisaną zestawieniem

i t^ci3 • ^Gi i.

gdzie: [CjJ - zbiór wartości cechy C_± /repertuar/ oznaczamy również jako W¹, G_± - graf, wierzchołki którego oznaczono elementami z [Cj |

Łuki grafu    wskazują no dopuszczalną kolejność zmian war

tości cechy G_t . W przypadku, kiedy kolejności tej ustalić nie można lub jest ona dowolna, należy założyć, że mamy do czynienia z grafem pełnym. Jeżeli z danego wierzchołka grafu    wycho

dzi więcej niż jeden łuk, to może zaistnieć potrzeba określenia warunków, przy których bieżąca wartość cechy może ulec zmianie na jedoą z następnych alternatywnych wartości /por. 3*3*4/.

Graf zmian wartości cechy określa indywidualnie dopuszczalne sek- I wmncje wartości, jakie może przyjąć dana cecha. Należy więc oc I do modelu poprawnego funkcjonowania    rozpatrywanego zasobu. I

Ponieważ cechy zasobu dzielimy na wyjściowe i wejściowe, in- I terpretacja przestrzeni wartości cechy musi uwzględniać równie! I i ten fakt, że wartości cech wejściowych są ustalone przez od- | działywanla zewnętrzne, natomiast wartości cech wyjściowych sl uzależnione od struktury zasobu 1 "historii" oddziaływań zewnętrznych. Zestawienia < [Cj ,    G^> dla wszystkich cech zasobu

łączni# tworzą układ wymiarowy przestrzeni cach takiego zasobu.

Ze względu na dyskretny charakter repertuarów wartości cech, » każdej chwili czasu zasób może być opijany wektorem wszystkich jego aktualnych wartości cach. faktor tan będziemy nazywać polnym ataoaa zasobu /przez analogię do modelu cybernetycznego/, & tell wektor zawiera tylko wartości cech wyjściowych zasobu, to *>f dziany S° nazywać stanem zasobu*

W celu opisania zmian stanów zasobu posłużymy się pojęciem iloczynu kartę z fańskiego grafów zmian wartości cech 'rJkloajct. W tym celu graf G^ cechy przedstawimy w pojtacl z*wt*. wienia

gdzie:    V¹ = |f_Ł] , T¹ - sygnatura, która każdemu elementowi

ze zbioru [Cj przyporządkowuje dowolny podzbiór tego zbioru. Iloczyn kartezjański grafów    będzie mieć postać

G — x Gg x • • • x Ggj ,

gdzie:    G = < V, F >

g₁ | < v<? , r¹ > , g₂ = <v² , r²>,..., 1 =<v" , r">

V | V¹ X V² X...X p    | V²,..., v“) /v£ i v|| k. 1,2,...,

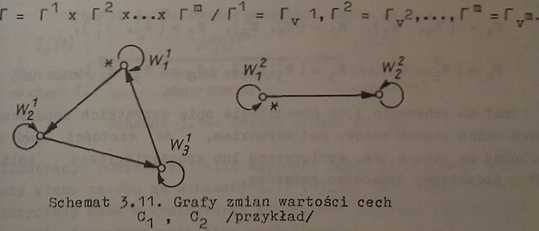
Na schemacie ąMi przedstawiono przykładowe grafy zmian wartości dwu cech 0^ oraz Cg. a na schemacie 3*12 graf będący ich iloczynem kartezjańskim. Przyjęto następujące oznaczenia: