DSC07024 (4)

36

^0fM liczbo*

36

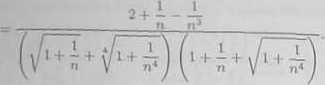
Stąd om * twierdzeń o arytmetyce granic otrzymamy

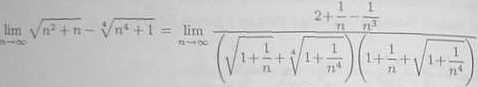
2+0-0 1

(v/i+o-r^t+ó).(i+o+yr+o) 2'

0 W rocwiązaniu zaztosujeray tożsamość

n| = Id • (Ar +1) •... * (n — 1) • n, gdzie 0 ś,k < n.

Możny zatem

(0^a+l)(2n-I}l    (np+1) (2n - 1)!    n^a +1

P«+ 1 +1    ⁼ (2« ~ t)K2n)(2n + 1) +1 = C* - Ul ₂„(2n-rl)^-^

glf

^L_ nż*

■** 2f2 + iV+_^l—

V W    l’)l

Stad om z twierdzeń o arytmetyce granic otrzymamy

(WV+t)(2*-i)ł    ^l|,+ ^r    +    _ i ¹

(2n+!)! +1    i!t₂/₂₊ i\.    I    %

V n/ n*(2n-l)!

• Przykład 1.8

Korzystając z twierdzenia o trzech ciągach znaleźć podane granice:

shr n + 4n a) lun —=r—— . •-•o. 3n —-1	b) liro R—OC	y/3* + 4^n + 5^n;	c) lim + 3; n—co
d) lim Vn+T;	e) lim	J1 2 3 n	f*) lim C/sin
•—OB	R—OG	V 2 3 4 n+1	W ‘OO V
	^ 4	+. ^1 V	h« ,w
«>-S* 1,7^7!^+	Vn^2 + 2	Vn^3 + n / '	^h * .JiSo logo (4.^n + U
,v ... / l	l ,	Hb \
Vf« +1)*	(n + 2)!		j) lim ^5" — 3^,ł — 2 • n—co

Przykłady

37

Rozwiązanie

Przypomnimy twierdzenie o trzech ciągach*. jeraU ciągi Wf. (bu). spełniają my-nająć od pewnej bezby nalunbte) no nierówności a.^li.^c.l skrajne ciągi (•*). (c^i są zbicinc do tej samej granicy, to ciąg środkowy jon równin lUeany do tej granicy, a) Zauważmy najpierw, «0$ an^ł n ^ Ul# każdego n(K Stąd

dla każdego n(N

0 + 4n sin³ n + 4n l + 4n

3n-l* 3n — 1 ** 3n-l

Ponieważ

*ln 4    ..

ura -    . = -z oraz lim

•»—oo 3n — l    3    * ■—

więc z twierdzenia o trzech ciągach wynika, że

„ sin² n + 4n

lun —r-;— =

•» -oo 3n — i

1-f 4n

3n - 1

4

3'

1

3'

b) Zauważmy nnjpli.-rw, że dla każdego n 6 N mamy

6 = WT o + 6" < V3"+4"+i" $ VF?F+F = &'VŁ

Ponieważ lim 5 = 5 oraz lim 5 V5 = o, więc z twierdzenia o trzech ciągach wynika, ir

lira + 4* + 5* = 5.

c)    Dla każdego n ^ 3 spełnione aą nierówności 1 $ Vn + 3 ( yfn 7 n =    ■ y/n. Qągi

ograniczając badany ciąg są zbieżne do 1. Żalem z twierdzenia o trzech ciągach wynika, że ciąg ten jest zbieżny do 1.

d)    Dla leaidrgo n ^ 2 prawdziwa jest nierówność n³^n+l. Zatem spełnione ząnierówności 1 $ "J/nTT $ Vn*. Ciągi ograniczające badany ciąg są zbieżne do 1. Żalem z twierdzenia o trzech ciągach wynika, żc

Em +i a i.

'■-•O#'.

c) Zauważmy najpierw, te dla każdego k € N prawdziwa jr*t nierówność jpr-y < I-Mamy zatem    _    i

JL...    ^: "

Ponieważ Um ?/i = 1 oraz lim tfn = l, więc z twierdzenia o trzech ciągach wynfra. y 2    a—oo

żc    ^___

lim _T/i ₊ | ₊ 2 ₊ ... ₊ 4T=l.

.

f*) W rozwiązaniu wykorzystamy nierówność sinx $ I dla r € R oraz sin z ^ -x dla ^x € [0.    . Mamy zatem