DSC07141 (6)

210

Całki

^0znac*one

Rozwiązanie

Wartość średnia funkcji / na przedziale [a,6| wyraża się wzorem

I nm

a)    Wartość średnia funkcji /(*) = e¹ na przedziale [—2,2) jest równa

/ = —i- [e* dx=- fe^rl^a = — ~ ¹

^/fc 2-(-2)7    4    <lc²

—2

b)    Wartość średnia funkcji g(x) = - *-y na przedziale [-1,0| jest równa

^ = ot|zI) / rrr ^=/(^{l +}    ) ^ = [*⁺I* -¹1] °__t =

-i    -i

c)    Wartość średnia funkcji /i(z) = sin³ z na przedziale [0, ir| jest równa

sin³ z dx.

1 +ln2.

K.    ^{Ałr =} -/‘

Ponieważ

/sin³zdz = ysinx(l — cos³z) dz

COS Z = u — sin zdz = du

= — J (l -u^ł) du = -u + y +(

= -cos _X + ^4^£ + C,

więc szukana wartość średnia jest równa

ml*

sin³ z dz = —

-C06Z +

_4_

3ir'

d) Mamy

•    ■1- z², do b —7xdx

*    = 0, V B 1

l/S 1

k„ =

_    | f zdz

W T ⁰

Przykłady

211

• Przykład 8.9

Samochód od chwili startu poruszał się ruchem jednostajnie przyśpieszonym z przyśpieszeniem aj = 2m/s . Po tj = 10 s zaczął poruszać się ze stalą szybkością. Po dalszych tj = 60 s zaczął hamować z opóźnieniem aj = 1 m/s^a aż do zatrzymania. Obliczyć średnią szybkość tego samochodu;

Rozwiązanie

Szybkość w ruchu jednostajnie przyspieszonym (opóźnionym) z przyspieszeniem (opóźnieniem) a rozpoczynającym się z szybkością początkową Vo jest określona wzorem v(t) = ud + ot (v(i) = uo — ot). W rozważanym przypadku mamy

( 2t dla 0 $ t $ 10, v(l) = ^ 20 dla 10 < t $ 70,

( 90-t dla 70 < t $ 00.

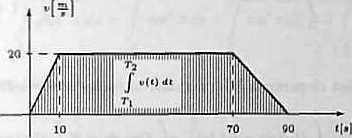
Szybkość średnią obliczamy ze wzoru 12

wdt

v = 5rW^w

10    70    W

1500    50    ... .

⁼ -*r⁼T^al6’^,m/S-

90

= &/u(t)dt= —

J 2t dl + j 20 dt + y (90 — t)dt .o    io 70 M. Mi

• Przykład 8.10

Pociąg jadąc ze zmienną szybkością przejechał 400 km w czasie 4 godz. Uzasadnić, że w pewnej chwili jego szybkość wynosiła lOOkm/godz.

Rozwiązanie

Niech s(i) oznacza drogę przebytą przez pociąg w czasie ł. Z warunków zadania mamy s(0) = 0, s(4) = 400. Szybkość pociągu w chwili t jest równa a'(t). Więc

1

J u(t) dt = J *'(t) dt = «(4) - a(0) = 400. o    o

Z drugiej strony, wobec twierdzenia całkowego o wartości średniej, mamy ■mmmm