DSCN0784 (2)

AA', AB i BB\ Jeśli mamy trzy boki trapezu i w dodatku wiemy, że trapgj ten jest prostokątny, to potrafimy go zbudować na płaszczyźnie rysun&u W 4-236). Z punktów A’ i B' poziomego rzutu odcinka AB wystawiamy prosto. J padłe do tego rzutu i odkładamy na nieb odcinki A'A i B'B równe odpowiedni) i A"A_x i B"B_X. Łącząc A_x i B_x otrzymamy rzeczywistą długość odcinka 4$; w kładzie na rzutnię poziomą jr_x. Widzimy z powyższego, że trapez ABB'4¹ został obrócony dookoła boku A'B' i doprowadzony do kładu na rzutnię pozioma, W ten sposób możemy również znaleźć rzeczywistą długość odcinka metody kładu na rzutnię pionową.

Do znalezienia rzeczywistej długości odcinka AB metodą obrotu (rys. 4-24)

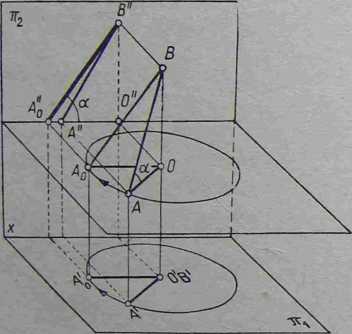
Rys. 4*24. Wyznaczanie rzeczywistej długości odcinka metodą obrotu

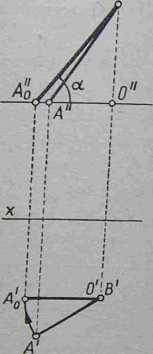
postępujemy w następujący sposób. Obieramy oś obrotu prostopadłą do rajSa poziomej i przechodzącą przez jeden koniec odcinka, np. przez punkt B. Ob& camy dalej odcinek AB do położenia A₀B równoległego do rzutni pionowi' Po dokonaniu takiego obrotu rzut poziomy A'₀B' zajmie położenie róy^⁰" legje do osi x, a wtedy rzut pionowy A'₀'B" będzie równy rzeczywistej dług^ odcinka. Kąt a jaki tworzy rzut pionowy A'₀'B" z osią x, jest kątem pochyl j nia danego odcinka do rzutni poziomej.

4.3. ODWZOROWYWANIE PŁASZCZYZN I FIGUR PŁASKICH 4.3.1. Ślady płaszczyzny

Położenie płaszczyzny w przestrzeni może być wyznaczone przez: a) punkty nie leżące na jednej prostej, b) prostą i punkt nie leżący na niej, c) ^ przecinające się proste, d) dwie proste równoległe.

Odwzorowania rysunkowego płaszczyzny najlepiej dokonać za pomocą linii przecięcia płaszczyzny z rzutniami. Na rys. 4-25 przedstawiona jest dowolna płaszczyzna a przecinająca rzutnię poziomą i pionową, linie, wg któ-

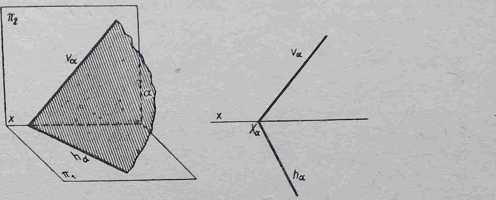
Rys. 4-25. Ślady dowolnej płaszczyzny

Tych płaszczyzna a przecina się z rzutniami, nazywamy odpowiednio: śladem poziomym h_a i śladem pionowym v_a. Oba ślady przecinają się w jednym punkcie X_a, który leży na osi rzutów x.

' Szczególne położenia płaszczyzn względem rzutni mogą być następujące: a) płaszczyzna mająca położenie dowolne (omówiona wyżej), b) płaszczyzna prostopadła tylko do jednej z rzutni, zwana dalej płaszczyzną rzutującą, i c) płaszczyzna prostopadła do dwu rzutni, tj. równoległa do trzeciej.

4.3.2. Płaszczyzny rzutujące

Płaszczyznę prostopadłą do rzutni poziomej jrj nazywamy płaszczyzną poziomo rzutującą (rys. 4-26). Pionowy ślad tej płaszczyzny jest prostopadły do osi x, a ślad poziomy tworzy z osią * kąt równy kątowi nachylenia tej płaszczyzny do rzutni pionowej

Płaszczyznę prostopadłą do rzutni pionowej n₂ nazywamy płaszczyzną pionowo rzutującą (rys’. 4-27). Poziomy ślad tej płaszczyzny jest prostopadły do

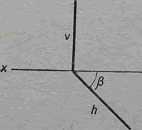
Rys. 4-26, Ślady .płaszczyzny poziomo rzutującej

Rys. 4-27. Ślady płaszczyzny pionowo rzutującej

Sti	K i
h .	WBSgm i / l

Rys, 4-28. Ślady płaszczyzny bocznie rzutującej

Osi ac, a ślad pionowy tworzy z osią x kąt równy kątowi nachylenia tej płaszczyzny do poziomej rzutni 7t_x.

69