S6300957

Mamy ^ (^Un) -i^es*' rosnący. Uzasadnimy teraz, że ciąg ten jest ograniczony z góry.

2 _ 2² 2³ 2"

3 + 1 ⁺ 32 + 2 ⁺ 3³ + 3 ⁺ ' •' ⁺ W+7i

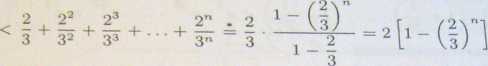
Pokazaliśmy, że badany ciąg spełnia założenia twierdzenia o ciągu monotonicznym i ograniczonym, a zatem jest zbieżny.

Uwaga. W miejscu oznaczonym (*) korzystaliśmy ze wzoru na sumę n początkowych wyrazów ciągu geometrycznego

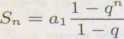
e) Korzystając z indukcji matematycznej * pokażemy, że ciąg (to_n) jest malejący, tzn. dla n 6 N spełnia nierówność vj_n+i < w_n. Mamy

wi = 3 > -102 = v^9.

Zatem nierówność io_n+i < tu» zachodzi dla n — 1. Niech n będzie dowolną liczbą naturalną. Załóżmy, że zachodzi nierówność io_n+i < u>n- Pokażemy, że wówczas zachodzi także nierówność io_n-(-2 < to_n+i ■ Rzeczywiście, mamy

10n+2 = y/wn+l + 6 ^    < \/w_n + 6 = W_n+i-

Z zasady indukcji matematycznej wynika, że nierówność io_n+i < w_n jest prawdziwa dla każdej liczby naturalnej n. To oznacza, że badany ciąg jest malejący.

Ograniczoność od dołu tego ciągu wynika z faktu, że jego wyrazy są dodatnie. Z twierdzenia o ciągu monotonicznym i ograniczonym wynika, że ciąg (io_n) ma granicę. Oznaczymy ją przez g i obliczymy. Przechodząc z n do nieskończoności w równości

tUn+l — VWn+6

oraz korzystając z twierdzeń o granicy sumy i pierwiastka otrzymamy równanie

9 - y^ + 6.

Równanie to po przekształceniach przyjmuje równoważną postać

g³ - g - 6 = 0.

Łatwo sprawdzić, że jedynym pierwiastkiem rzeczywistym tego równania jest g — 2. Zatem lim w_n = 2.

n—*oo

f*) Pokażemy, że ciąg (v_n) jest rosnący. Rzeczywiście, dla n 6 N mamy

fn_+l = Vn (l + —^Tt) > «"•

‘Twierdzenie o indukcji matematycznej wraz z przykładami można znaleźć w podręczniku „Wstęp do analizy i algebry. Teoria, przykłady, zadania