DSCN0789 (2)

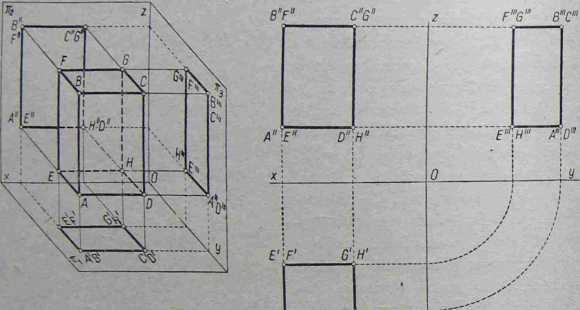
Połączenie odpowiednich rzutów tych punktów liniami prostymi da trzy płaskie figury w kształcie prostokątów: 1) w rzucie pionowym ściana widoczna z przodu pokrywa również tylną ścianą, b) w rzucie bocznym ściana widoczną

t!W~ OT " V

Rys. 4-49. Prostopadłościan w rzutach na trzy rzutnie

z boku lewego pokrywa również ścianę boczną z prawej strony, c) w rzucie poziomym ściana widoczna z góry pokrywa również podstawę prostopadłościanu.

Rys. 4-50 przedstawia graniastosłup o podstawie sześciokąta foremnego ustawiony w poziomej płaszczyźnie rzutów w sposób najkorzystniejszy względem płaszczyzn rzutów. Rzutowanie rozpoczynamy od rzutu poziomego, po-

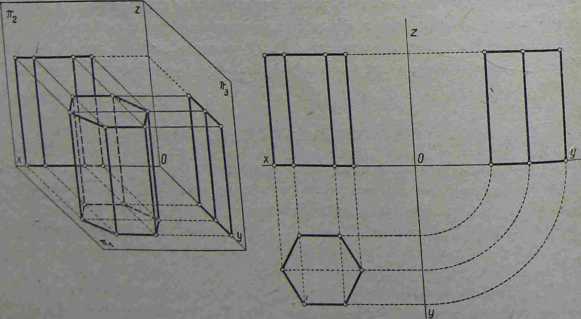
Rys. 4-50. Graniastosłup w rzutach na trzy rzutnie

nieważ ten rzut będzie rzeczywistą wielkością obu podstaw. W rzucie pionowym tylko dwie ściany należące do powierzchni bocznej graniastosłupa będą równe rzeczywistej wielkości jego ścian, ponieważ zajmują położenie równoległe do pionowej płaszczyzny rzutów, pozostałe zaś zajmują położenie skośne względem płaszczyzn pionowej i bocznej, będą więc w skrócie.

Rys. 4-51 przedstawia w rzutach ostrosłup o podstawie kwadratowej stojący na poziomej płaszczyźnie rzutów. Rzutowanie rozpoczynamy od wyznaczenia rzutu poziomego, następnie pionowego i wreszcie bocznego. Widzimy tu przykład bryły w rzutach, z których rzuty pionowy i boczny są jednakowe.

Na rys. 4-52 przedstawiono rzuty walca' ustawionego na poziomej płaszczyźnie rzutów. Rzut poziomy takiego walca jest kołem o średnicy równej

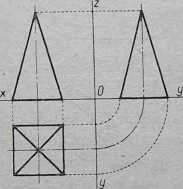
Rys. 4-51. Ostrosłup w rzutach na trzy rzutnie

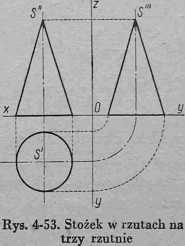
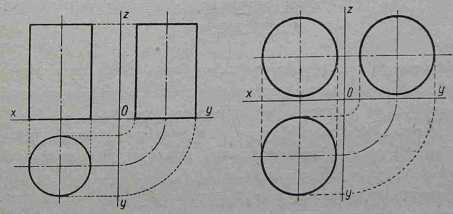
Rys. 4-52. Walec w rzutach na Rys. 4-54. Kula w rzutach na trzy rzutnie    trzy rzutnie

rzeczywistej średnicy podstawy walca, rzuty zaś pionowy i boczny są prostokątami, których podstawy są równe rzeczywistej wielkości średnicy walca, a wysokość rzeczywistej wysokości walca.

Rys. 4-53 przedstawia rzuty stożka ustawionego na poziomej płaszczyźnie rzutów. Rzut poziomy jest kołem o średnicy podstawy stożka, rzut pionowy i boczny są trójkątami równoramiennymi, których wysokość jest równa

79