DSC07380

178

Krzywe stożkowe

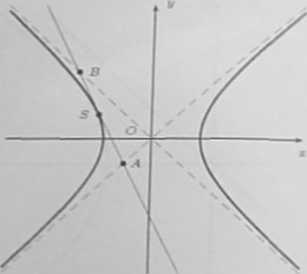
Współrręóne tych punktów spełniają zatem odpowiednio układy równań:

wi

6³

= 1,

{Si _ 511 — i    ( Si

-^a;⁶²« 1 ”^mz^x- U=

Roe wiązaniami tych układów są pary

1 1	fx aPb
■* fcri — oyi' 1 alP	° h*j + oyi ’ -ab-
^9* fcr, - oy,' 1	[ ^Ja kt| + ayi'

tfi

₌ V_A +Vj,

Łatwo sprawdzić, że zachodzą równości *« =

To oznacza, że punkt S = (zi.pi) jest środkiem odcinka AB, co mieliśmy pokazać.

Parabola

Przykład 6.7

a)    Podać współrzędne ogniska oraz równanie kierownicy paraboli y¹ = 6*;

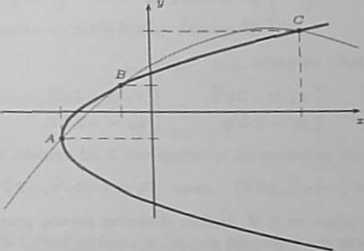
b)    Parabola przechodzi przez punkty A = (-3,-1), 13 = (—1,1), C = (5,3). Znaleźć równanie tej paraboli;

c)    Znaleźć współrzędne wierzchołka oraz równanie osi symetrii paraboli

y² + 10y-4x + 21 = 0;

d)    Sa paraboli y² = -2r znaleźć punkty położone w odległości 5 od ogniska;

•) Znaleźć miejsce geometryczne środków cięciw paraboli y — x~, które przechodzą przez punkt A = (0,1).

Rozwiązanie

a) Wykorzystamy fakt, ze parabola y² = 2px ma ognisko F = (p, 0) ornz kierownicę

przykłady    ¹⁷⁹

. * s -p. Z powyższego wynika, że parabola y¹ = 6* ma ognisko F = (3,0) oraz loerownicę k: z = —3.

b) W zadaniu nie określono, czy parabola ma równanie postaci

(y — yo)^a = 2p (z - zo),

czy też

(z — zo)' = 2p (y - yo).

Rozwiązanie podamy tylko dla pierwszego przypadku. Podstawiając współrzędne punktów A, B, C do równania paraboli otrzymamy układ równań z niewiadomymi zo,yo,p :

I (—1 — yo)² = 2p (—3 — zo),

I (1 — yo)^a = 2p (—1 — zo) |

H(3-yo)^a=2p(5-xo).

Jedynym rozwiązaniem tego układu jest trójka

zo = —3, yo = —1, p= Ł „-Zatem równanie paraboli ma postać

(y + i)^a = 2(x + 3).

Postępując w podobny sposób w drugim przypadku otrzymamy parabolę

(*-4)’f).

y¹ + lOy — 4i + 21 = 0

c) Równanie przekształcimy do postaci

(y “ yo)³ =2p(z — Zo),

z której łatwo można odczytać potrzebne wielkości. Mamy

y^ł + lOy — 4z + 21 = (y - 5)^a - 25 - 4x + 21 = (y - 5)^a - 4z - 4 = 0.

Zatem równanie paraboli można przepisać w postaci

(y-6)^ł =*4(x + l).

Wierzchołek W paraboli ma zatem współrzędne (—1,5), a oś symetrii równanie y = 5.

d) Parabola o równaniu y^a = — 2i ma ognisko F = (—1,0).