DSC07379

176

Krzywe stożkowe

Rozwiązanie

a) Równanie stycznej hiperboli równoosiowej xp — c, w punkcie (xi,pt) m* postać:

yt(x — *1) + *1 (p — Pi) = 0.

Przyjmując w tym równaniu (zi.yi) = (2,6), otrzymamy

6(x — 2) + 2(p — 6) = 0.

3x + p - 12 = 0.

Zatem styczna ma postać b) Równanie stycznej do hiperboli

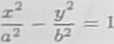
w należącym do niej punkcie (xi,pi) ma postać

jgi _ PPl _ _x

P

Zatem równanie stycznej do rozważanej hiperboli będzie miało postać

4xxj — yyi = 4.

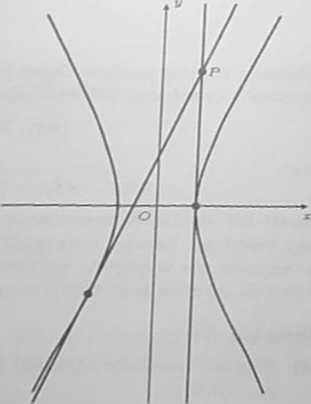
Ponieważ styczna ta przechodzi przez punkt P = (1,4), więc

4xi — 4pj = 4.

Ponadto, punkt (xt.pi) należy do hiperboli. więc spełnia jej równanie

4*?-p? = 4.

Otrzymaliśmy układ równań

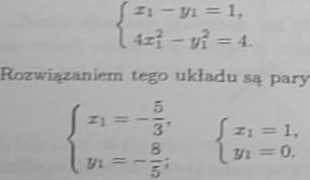
Podstawiając otrzymane rozwiązania do równania stycznej otrzymamy następujące styczne

5x — 2p + 3 = 0, z = 1.

e) Niech P = (xi,.pi.) oznacza punkt prawej gałęzi hiperboli. Punkt P będzie położony najbliżej preatej p = z, gdy styczna do hiperboli w tyrn punkcie będzie równoległa do prostej.

Przykłady

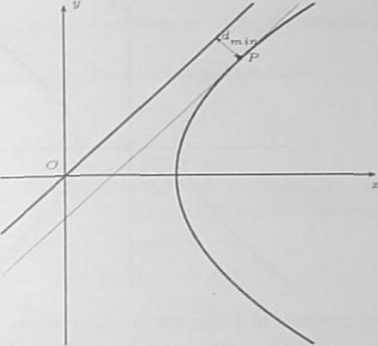
Wynika to z Taktu, że prawa gałąź hiperboli jest „brzegiem” zbioru wypukłego na płaszczyźnie Prosta przechodząca przez punkt (*1,2/1), która jest równoległa do prostej y = *, ma postać

y — yi = * — *1.

Z drugiej strony styczna do hiperboli w punkcie (*1,2/1) ma postać

XXI

10

Vl/i

= 1.

Porównując współczynniki przy zmiennych x,y otrzymamy układ równań

9*i — 16j/i = 0,

2/i — 3:12/1 +9 = 0.

Rozwiązaniami tego układu są pary

16

^{Xl =} v^’

9

■ 16 ® ⁼

0

Ponieważ punkt P należy do prawej gałęzi hiperboli, więc pierwszą parę odrzucamy. Zatem punkt P =    jest położony najbliżej prostej y = *.

d) Niech punkt S = (n.ji) należy do hiperboli o równaniu

4-£=i.

o⁷ 6*

Równanie stycznej do hiperboli w tym punkcie ma postać

**1

n3

t/gl

6?

= 1.

Dalej niech A, B oznaczają punkty przecięcia stycznej hiperboli z jej asymptotami.