DSC07373

164

Krzywe stożkowe

b) W rozwiązaniu wykorzystamy następująca charakteryzację stycznej do okręgu: prosta jest styczna do okręgu wtedy i tylko wtedy, gdy ma z nim tylko jeden punkt wspólny. Równanie prostej przechodzącej przez punkt P = (2,0) ma postać y = m(x — 2), gdzie m € R. Prosta ta będzie styczna do rozważanego okręg, gdy układ równań

y = rn(z — 2),

(x+l)^ł+y* = l

miał tylko jedno rozwiązanie. Układ ten po prostych przekształceniach przyjmie

postać

V — ^m(^x -¹)>

(m² + l) x² + (2 — 4m²) x + 4m² = 0.

Aby otrzymany układ miał tylko jedno rozwiązanie drugie z równań, tj. równanie kwadratowe z niewiadomą x i parametrem m, także musi mieć tylko jedno rozwiązanie. Tak hęAióf, gdy wyróżnik równania kwadratowego będzie równy 0. Mamy zatem

A = (2 - 4m*)^S - 4 • 4m^s (m² +1) = 4 - 32m² = 0.

Stad m = — lub m = ——. Styczne do okręgu mają równania 4    4

y = ^(*-2). y = -|(*w2).

c) Ponieważ szukany okrąg jest styczny do osi układu współrzędnych i przechodzi przez punkt położony w drugiej ćwiartce, więc jego środkiem jest punkt S = (—r,r), gdzie r > 0 jest promieniem okręgu.

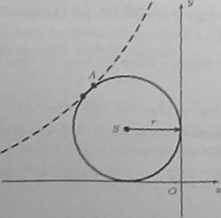
Równanie tego okręgu ma postać

Przykłady

165

Ponieważ punkt A = (-8.9)    ^{do okr}®^u- ^wi*^c

(—8 + r)³ + (9 — r)³ = r³.

Stąd    _

r³ — 34r +145 = 0.

Pierwiastkami otrzymanego równania kwadratowego są

ri =6, rj = 29.

Istnieją zatem dwa okręgi spełniające warunki zadania:

(* + 5)³ + (y - 5)³ = 5³,    (* + 29)³ + (y - 29)³ = ₂9³

*

d) Zauważmy, że punkt okręgu będzie położony najbliżej (najdalej) od prostej, gdy styczna do okręgu w tym punkcie będzie równoległa do prostej. Prosta równoległa do prostej y = x -|- 5 ma Postać y — x + 6, gdzie 6 6 R. Aby prosta ta była styczna do okręgu, odległość wódka okręgu, tj. punktu (0,0), od niej powinna być równa promieniowi okręgu ^{r =} v/2. Korzystając ze wzoru na odległość punktu Po = (xo,yo) od prostej t: Ax+By + C = 0;

d(Pb l) = ^1/1 J° + Byg+Cl y/A* + Bⁱ '

otrzymamy

|0-0 + 6| _._/5 \A³ + (-l)³

Stąd 6=2 lub 6 = —2. Łatwo sprawdzić, że punkt styczności Pi = (—I, j) prostej V = x + 2 i okręgu realizuje najmniejszą odległość, a punkt Ą = (1,-1) największą.

sprawdzić, że okrąg o równaniu

x³ — 2x + y³ + 4y = 0

ma środek 5 = (1, —2) oraz promień r = V&. Rozumując podobnie jak w przykładzie d) otrzymamy, że prosta = 2x + 6 będzie styczna do okręgu

x³-2x + y³ + 4y = 0.

gdy odległość środka okręgu od niej będzie równa promieniowi. Stąd mamy równanie

|2-ł-(-₂) ₊ 6|    ^

•W

Po prostych przekastałceniaeb otrzymamy

|6 + 4| = 5.