DSC07374

166

^Kr*ywe stożkowe

Stąd b = 1 lub 6 = —9. Szukane styczne mają zatem równania p = 2z +1, y = 2x — 9.

f) Z faktu, że proste y = x - 1, p = z + 3 są równoległe wynika, że promień szukanego okręgu jest równy połowie odległości między nimi.

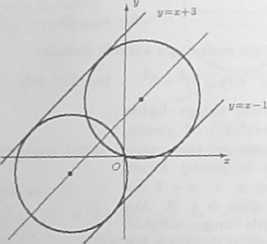
Odkgłcść prostych równoległych

łj: Ax t By + Ci = 0, l? : Ax + By + Cj = 0

wyraża się wzorem

d{tuh) =

[Ci —Cą|

>/F+F'

Zatem mamy

i

: = t/Ł

J² Vi^a+C-i)²l

Znajdziemy teraz współrzędne (zo.po) środka okręgu. Punkt ten jest położony w jednakowych odległościach od prostych y — i — 1, y = z+3. Korzystając ze wzoru podanego w rozwiązaniu przykładu d) otrzymamy warunek

|xp - po - 1| _ |xo-pn + 3| yJV + (-1)* v'l² + (-l)^J'

Stąd jo = zo + I. Szukany okrąg ma zatem równanie

(x - *o)^ł + (p - (*0 +l))² = (i/2)².

Ponieważ początek układu należy do okręgu, więc

*o + (*o +1)^{2 =} 2.

Stąd

xo = -₅--_r lub xo =

Przykłady

167

Ostatecznie rozważany okrąg ma równanie

+

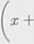
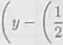
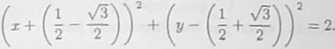
Elipsa

• Przykład 6.3

a)    Znaleźć równanie elipsy o wierzchołkach K = (-1,3), L = (5,3), U = (2,1), V ⁼ (?i 5);

b)    Początek układu współrzędnych jest środkiem elipsy o osiach symetrii Ox i Oy. Znaleźć długości osi tej elipsy, jeżeli wiadomo, że przechodzi ona przez punkty A = (1,2),B = (-3,1)_:.

c)    Obliczyć osie, ogniskową i mimośród oraz wyznaczyć współrzędne środka i ognisk elipsy 9ar + 36a: + 25y - 50y - 164 = 0;

d)    W elipsę — + 7- = 1 wpisano kwadrat o bokach równoległych do osi układu

y 10

współrzędnych. Obliczyć współrzędne wierzchołków tego kwadratu;

^e)    Koło K\ jest zawarte w kole Kj. Pokazać, że miejscem geometrycznym środków kół stycznych zewnętrznie do koła Aj oraz wewnętrznie do kola Kq jest elipsa.

Rozwiązanie

a) Odległości między przeciwległymi wierzchołkami elipsy są jej osiami. Zatem

2a = \KL\ = ^(5 - (-1))² + (3 — 3)³ = 8 2b = IWI = y/(2-2)³ + (S - l)³ = 4.

środek S = (x_s, y_a) elipsy leży w połowie odcinków łączących przeciwległe wierzchołki.

I®    w. i—1 + 5 i    3 + 3    ,

x, = —j— f² onz K» = ~2~=³-

Znając osie oraz współrzędne środka elipsy możemy napisać jej równanie

(a=-2)^a (y — 3)^ł 3-^:    2¹

b) Równanie rozważanej elipsy ma postać

= 1.