DSC07376

170

Krzywe stożkowe

d) Wyznaczyć równania wspólnych stycznych elips

x³ + 6y²=6, 9x^a + 4y² = 36.

Rozwiązanie

a) Znajdziemy najpierw punkt styczności (p,p), gdzie p > 0. Mamy 3

Stąd p =    — Wykorzystamy teraz równanie

Vl0

2 2 5- + Ł = l

o^{3 +} 6*

stycznej do elipsy w punkcie (ii.jn) elipsy. Mamy

H

^XyT5 , 3y _ i

9 ^lÓ ’

stąd

x + 9y - 3VT0 = 0.

b) W rozwiązaniu wykorzystamy własność: prosta jest styczna do elipsy wtedy i tylko wtedy, gdy ma z nią dokładnie jeden punkt wspólny.

Prosta przechodzącą przez początek układu ma równanie y = mx, gdzie m € R. Z przytoczonej własności wynika, że prosta la jest styczna do elipsy

x^a — 6z + 4y² + 5 = 0

wtedy i tylko wtedy, gdy układ równań

(y= rai,

\ x* + 8x + 4y* +5 = 0    _

Przykłady

171

m tylko jedno rozwiązanie. Po prostych przekształceniach otrzymamy równoważną postać układu

| V = mx,

| (Am¹ + l)z³ + 6z +5 = 0.

Układ ten będzie miał jedno rozwiązanie, gdy drugie z równań (równanie kwadratowe z niewiadomą z i parametrem rn) będzie rniało jedno rozwiązanie. Tak będzie, gdy wyróżnik równania kwadratowego przyjmie wartość 0. Mamy

A = 6^S —4-5- (W + l) = -16m² + 20 = 0,

stąd m = — lub m = —

Równania stycznych mają zatem postać

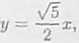
V = ~

y/E

2 *•

c) Prosta równoległa do prostej y = 2x ma postać y = 2z+6, gdzie 6 e S. Wykorzystamy własność podaną w rozwiązaniu przykładu b). Z własności tej wynika, że prosta y = 2x+b będzie styczna do elipsy

4x^s+5y²=120,

gdy układ równań

f y = 2x + b,

1 4x² -I- 5y² = 120

będzie miał tylko jedno rozwiązanie. Tak będzie, gdy równanie kwadratowe, w równoważnej postaci układu

f y = 2x + b,

1 24x² + 206* + 56* - 120 = 0, będzie miało zerowy wyróżnik. Zatem

A = (2Q6)^a - 4 • 24 (56² - 120) = -806² +11520 = 0,

stąd

6 = 12 lub 6 =-12.

Styczne do elipsy mają zatem równania

y = 2x +12, y = 2z -12.

d) Niech y = mi + 6 będzie wspólną styczną obu elips (rysunek).