DSC07381

ISO

Krzywe stożkowe

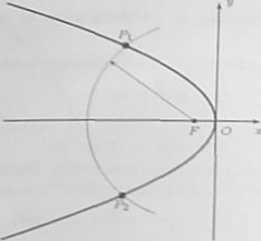
N«= P = (z.|) wwm punkt paraboli położony w odległości 5 od jej ogniska. Wówczas

ipdBOOjr jEtf tdiid ióvoui

_%/(x+I)* + (y-0)» =5.

Po prostych |

otrzymamy równoważną postać układu

fsr = -2x.

1 »^ł = -X³ - 2x + 24-

Sanąamrn tego ukisdu są puy;

f *« = -2^6, f x_a = -2v/fl,

U, =2^6; i m = -2 ^6.

Zam ponktaau prahoB położonymi w odległości 5 od ogniska są

Pl = (-2v'6.2$^,S) oraz ft - (-2t/6, -2^6) .

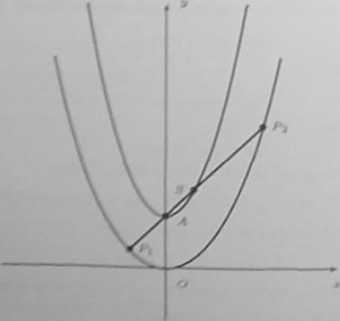
ej S«=d> y = tnx - I. gdzie m € 8, będzie dowolną prostą przechodzącą przez punkt A=(0.1,- Prosta ta przecina parabolę y = x² w punktach Ą i Pj.

Przykłady

181

Wyznaczymy środek S odcinka Pi Pi (cięciwy paraboli). Współrzędne (zi.yi), (zj.yj) odpowiednio punktów Pi, Pi są rozwiązaniami układu równań

/ y — mx+ l,

\y = x⁷.

Układ ten jest równoważny układowi

{ly = mi +1,

|i^ł- mz — 1 = 0.

Ponieważ współrzędne (x_s,y_g) środka S odcinka Pi Pi są określone wzorami

_ Zł -I- u __pi +10

®r 2    ¹ Va 2    ¹

więc nie ma potrzeby znajdowania rozwiązań ostatniego układu. Wystarczy znajomość sumy pierwiastków równania kwadratowego x² — mx — 1 = 0. Ze wzorów Vietc'a mamy

xi + X2 = m.

Stąd

m    . mi

x, = y oraz y_s = mi, +1 = -ęp +1.

Po wyrugowaniu parametru m otrzymamy zależność

y₈ =2x1 + 1.

Zatem środki cięciw tworzą parabolę

Ił = 2x^a + 1.

• Przykład 6.8

a)    Napisać równanie stycznej do paraboli (y — 3)² = 8(z + 1) wystawionej w należącym do niej punkcie P = (1,7);

b)    Znaleźć równania wszystkich stycznych do paraboli y = x² — 4x + 5, które wychodzą z punktu P = (3,0).

c)    Wyznaczyć równanie stycznej do paraboli i/² = —6x, która jest prostopadła do prostej x + 3y + 12 = 0;

d)    Pokazać, że styczne poprowadzone do paraboli z dowolnego punktu kierownicy są prostopadle.

Rozwiązania

a) Wiadomo, że równanie stycznej paraboli

(U-Do)¹ = 3p(*-xo)

w punkcie (xi, i/i) ma postać

(l/i - ?/o)(U - Vo) = p((*i - *o) + (* - *o)).