DSC07375

168

Krzywe stożkowe

Ponieważ punkty A i B należą do niej, więc ich współrzędne spełniają to równanie. Stąd otrzymamy układ równań

M+M₌₁

o* 6*    ’

i.

- a? ⁺ K*

Rozwiązaniem tego układu (wśród par liczb dodatnich) jest

■

Klipsa ma zatem osie

|a =    i 2b = <J

c) Przekształcimy równanie elipsy do postaci

(* - x₀)² , (y - yo)^a _ ,

~ a|    **

z której odczytamy potrzebne wielkości. Mamy

ftr³ + 36z + 25y² - 50y - 164 = 0 (*^a + 4x +4) + 25 (y² - 2y + l) - 38 - 25 - 164

= 9(x+ 2)^a + 25(y - l)² - 225 = 0.

Zatem równanie elipsy można przepisać w postaci

(* + 2)^a , (y-D^a ,

5*    ■    3*    ^_

Stąd widać, że elipsa ma osie 2a = 10, 25 = 8 i środek S = (—2,1). Możemy obliczyć teraz ogniskową 2c, mimośród e oraz współrzędne ognisk Fi, Fi. Mamy

2c = y/a² -6* = 2y/s* -Z² = 8,

_ c _4 ^C a ^— 5’

= (rro — ć,yo) = (—2 — 4,1) = (—6.1).

Fi = (xo + c,yo) = (—2 + 4,1) = (2,1).

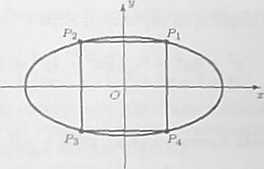
d) Niech 2d oznacza bok szukanego kwadratu. Z symetrii wynika, że wierzchołek Pi kwadratu, położony w pierwszej ćwiartce, ma współrzędne (d,d). Ponieważ należy on do elipsy, więc spełnia jej równanie. Mamy zatem

£ + £ = ,.

0 IB

Stąd d = -jr. Wierzchołkami kwadratu są punkty:

*=(¥•¥)• «-(-¥■¥)• «-(-¥•-¥)• «-(¥•'¥)•

Przykłady

169

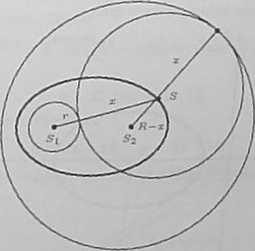
e) Niech kolo Ki ma środek Si i promień r, a kolo Ki środek Sj i promień R. Ponieważ Ki C Ki, więc r < R oraz |SiSj| < R — r. Ponadto niech S będzie środkiem ruchomego kola, które jest styczne zewnętrznie do kola Ki i wewnętrznie do kola Ki. Z warunków styczności mamy wówczas

|SSi| = r + x, |SSj| = R -x,

gdzie x oznacza bieżący promień kola o środku S. Pokażemy, że punkty S należą do elipsy

0    ogniskach Si, Si. W tym celu sprawdzimy, że suma odległości punktów S od ognisk Si

1    Si jest stała i większa od odległości miedzy ogniskami. Mamy

|SS,| + |SSz| = (r +x) + (R — x) = r + R = const

oraz

|SiSa| = R—r <r + R.

Otrzymaliśmy stalą sumę odległości od ognisk, zatem miejscem geometrycznym środków okręgów jest elipsa.

• Przykład 6.4

a)    Napisać równanie stycznej elipsy + y¹ = l w punkcie elipsy o jednakowych dodatnich współrzędnych;

b)    Znaleźć równania stycznych elipsy x³ — 6x + •!y³ + 5 = 0 wychodzących z początku układu współrzędnych;

c)    Znaleźć równania stycznych elipsy 4x³ + 5y³ = 120, które są równolegle do prostej u — 2x\