180

Stąd transformata prądu szukanego

Uo(*)    4*+2    4r+2    2r+l 2ł+l

“ Z„(s)+R " 2s+l+2s²+2s+i ⁼ 2s²+4r+2 " s²+2s+l    (r + 1)² '

Wartość chwilową prądu wyznaczamy na podstawie odwrotnego przekształcenia La-„ placek:

i-*-/(,)+    - *P-*r*+«- -

- 2e-^,-2^e-‘^-^e-^, = (2e-‘-te-*) A.

4.31. W obwodzie przedstawionym w rysunku przed otwarciem wyłącznika panował stan ustalony. Parametry elementów obwodu wynoszą: 2? * 30 V, / = 0,1 A, R_t - 100 Q, R₂ = 200 Q, i?₃ « 100 Q, £_s - 200Q, C₂ - C₄ « 100 pF. Obliczyć wartość chwilową prądu w oporniku i?₃ po otwarciu wyłącznika stosując twierdzenie Thevenina.

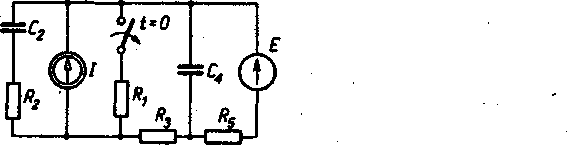
,    Ryt. do zad. 4.31

Odpowiedź, i. - (100 -80e-¹⁶-⁶*+30e-¹⁰⁰') mA.

4.2. SCHEMATY BLOKOWE 1 GRAFY PRZEPŁYWU SYGNAŁÓW

4.32. Dla obwodów elektrycznych przedstawionych na rys. a, b, c, d narysować schematy blokowe i obliczyć transmitancje operatorowe tych obwodów przez zwijanie jodpowiadających im schematów blokowych. Wielkości wejściowe i wyjściowe obwodów zaznaczono na rysunku.

Rozwiązanie, (a) Schemat rozpatrywanego obwodu w postaci operatorowej przedstawiono na rys. e. Schemat blokowy odpowiadający temu obwodowi rysujemy korzystając z równań Kirchhoffa [6 str. 167; 23]:

/(*) =

1

R+Ls

U₂(s),

U₂(s) = ±I₂(s),    I₂(s) =

U_R(s) = U(_S)-U₂(*).

Schemat rysujemy zaczynając od sygnału wyjściowego. Kolejno dochodzimy odpowiednio do prądów i napięć U₂,1₂,I₂, Ur, U. Wielkości te zaznaczono na schemacie elektrycznym i blokowym (rys. fj. Następnie zwijamy schemat blokowy. Przesuwając ♦

180,    .'. ^: