DSCN1131 (3)

§ 5. Rozwiązania i odpowiedzi

5.1. Zgodnie z oznaczeniami wprowadzonymi na rys. 5.1 mamy: | p POB\ — 60° — x, \<POA\ = x. | PA\ = b, |PB| = c.

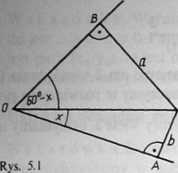
Rozpatrując trójkąty OAP i OBP mamy:

b__c

sin* sin (60° — x) ’ skąd

^by/3 cos* — -bsinx = c^sin*.

Stąd po prostych przekształceniach otrzymujemy

by/l

Ponieważ

2Jb² + bc + <

\OP\ =

b

sin*’

więc

\OP\ = ^ i(b² + bc + c²).

U w a g a. W szczególności, gdy punkt P należy do dwusiecznej kąta, to |0P| = 2b.

5.2. Wprowadzając oznaczenia jak na rys. 5.2 mamy:

\<BAC\ = 60°,\<ACB[ = 30°, ABJ.BC, \AC\ = 2x, \BC\Ś

S

Ponieważ okrąg <ĄO,r) jest wpisany w A ABC, więc r =

X

więc r = —7=-.

^3 + 1

Rozpatrując trójkąt prostokątny AD0₂> mamy:

ct R

\AD\ = x + R. \D0₂\ = R. tg- = ——czyli

/—    A, X T A

R =-

Wobec tego —5 = (2 — ^Z^)²-

5.3. Szkic rozwiązania.

Szukanym zbiorem punktów jest zbiór R\jW z rysunku 5.3.b). Do dowodu potrzebne jest twierdzenie pomocnicze:

Średnica okręgu jest widziana z punktu znajdującego się

-    wewnątrz okręgu pod kątem rozwartym,

-    na okręgu pod kątem prostym,

-    na zewnątrz okręgu pod kątem ostrym.

Łatwy dowód tego twierdzenia można oprzeć na rysunku 5.3.a). Zauważmy, że punkt styczności stycznej do danego okręgu o środku

0    przechodzącej przez punkt X należy do okręgu o średnicy OX. Jeśli teraz punkt X należy do zbioru R, to APAB zawiera się

* *

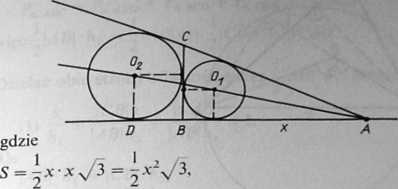
Rys. 5.2

p = i(x + x_s/l + 2x) = ix(3 + y/3),

(okręgu o średnicy XO,sl więc styczne wyprowadzone z punktu nie mają punktów stycznych z lukiem A&.

[jeśli punkt X należy do zbioru S, to \-%.XBO\ < 90°

1    \ -%.XAO\ > 90°, a więc okrąg o średnicy XO przecina luk AŚ.

119