DSCN1652 (3)

Indeks selekcyjny - technika obliczeń. Zastosowanie rachunku macierzowego do rozwiązania układu równań

Aby obliczyć współczynniki indeksu selekcyjnego należy rozwiązać układ równali (7.3). Równań jest tyle, ile źródeł informacji, zatem im większą liczbą źródeł informacji dysponujemy (między którymi najczęściej występują zależności), tym trudniejsze staje się uzyskanie rozwiązań: np. przy wykorzystaniu wydajności babki, matki, córki, pół! siostry i pełnej siostry (5 źródeł informacji, wszystkie ęfj różne od 0) rachunki są co najmniej żmudne, a jeśli uwzględni się dodatkowo obserwacje cech skorelowanych (nie tylko u osobnika, ale i krewnych), bądź średnie wydajności grup krewnych - stają się bardzo skomplikowane.

W takich sytuacjach do obliczeń lepiej zastosować rachunek macierzowy, umożli-l wiający uproszczenie zapisu matematycznego układu równań, a przede wszystkim-jednoczesne uzyskanie wszystkich rozwiązań (wartości współczynników a; lub bezpośrednio hj indeksu selekcyjnego).

Podstawy rachunku macierzowego

Macierzą nazywamy tablicę prostokątną elementów uporządkowanych w p wierszy i q kolumn:

“pi

^a12	ą
^a22 •	• ^alq
“pl ■	.. apq

^an

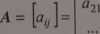
i

62