DSCF6547

50

Z porównania otrzymanej wartości x² = 12,88 z wartością krytyczną odczytaną w tablicach dla k = 9 i a = 0,05 wynika, że nie ma podstaw do odrzucenia hipotezy H₀ dla przyjętego poziomu istotności, ponieważ X² = 12,88 < x 9:0.05 = 16,92. W oryginalnej pracy połączono wszystkie prze-działy, poczynając od liczby przypadków wynoszącej 10, czyli dwukrotnie więcej od zalecanej wcześniej minimalnej liczebności. Rezultat testu pozostanie jednak niezmieniony również dla n_mta. = 5.

5.3.4. Przykład (testowanie hipotezy o wartości średniej)

yftl o rozkładzie N(0, 1). Gdyby znana była dyspersja

Producent proszku kserograficznego (tonera) utrzymuje, że średni promień ziaren wynosi 1,5/im; wariancji rozkładu nie podano. W laboratorium zmierzono promienie n = 10 przypadkowo wybranych ziaren, otrzymując wyniki na ogół większe od wartości nominalnej (w mikrometrach): 1,93, 1,67, 1,32, 1,70, 1,65, 1,43, 1,58, 1,47, 1,54, 1,54. Zakładamy wstępnie (jest to nasza hipoteza zerowa H₀), że promień ziaren x podlega rozkładowi normalnemu¹ z wartością średnią 1,5 /zm i nieznaną wariancją <rj, czyli H₀:xeN( 1,5, <rl). Konkurencyjna (alternatywna) hipoteza H_l mówi, że wartość promienia przewyższa 1,5 /zm: i/,: R eiV(/z,, <r«); /z₁>l,5/zm. Testowanie hipotezy zerowej polega na wyjaśnieniu, czy średnia z próbki wynosząca Tl = 1,583 /zm jest dostatecznie bliska 1,5 /zm, aby uzasadnić przyjęcie hipotezy zerowej. W takim wypadku zaobserwowane odchylenie wartości średniej próbki od postulowanej średniej populacji, byłoby traktowane jako następstwo niewielkich rozmiarów próbki. W innym wypadku różnica promieni świadczyłaby na korzyść hipotezy alternatywnej. Aby rozstrzygnąć te wątpliwości, rozpatrzmy statystykę _u _ (¹-/¹) _ n n

rozkładu a_x, wystarczyłoby sprawdzić, czy otrzymana wartość zmiennej u jest większa, czy mniejsza od wartości krytycznej, odpowiadającej np. poziomowi istotności a = 0,05. Ponieważ dyspersja pozostaje nieznana, możemy wykorzystać jedynie jej ocenę:

i rozważyć zmienną t, skonstruowaną analogicznie do zmiennej u:

Użyto oznaczenia t, ponieważ po zapisaniu ostatniego wyrażenia w równoważnej postaci:

rozpoznajemy w liczniku rozkład N(0, 1), zaś w wyrażeniu podpierwiastkowym w mianowniku Xn-i/(n—1), co spełnia wymagania określające zmienną Studenta (por. 3.13) dla k = n — 1 stopni swobody. Po podstawieniu odpowiednich wartości liczbowych otrzymamy w wyniku t= 1,56. W tab. 4 dołączonej do skryptu można dla konwencjonalnie przyjmowanego poziomu istotności a = 0,05 odczytać wartość krytyczną £_9;0.05 = 1,833 > 1,56. Otrzymana wartość trafia więc do obszaru akceptacji hipotezy testowanej. Zatem dla przyjętego poziomu istotności a = 0,05 nie ma podstaw do odrzucenia hipotezy zerowej mówiącej, że średni promień cząstek tonera wynosi 1,5 pm.

5.3.5. Przykład (przedział ufności dla wartości średniej)

Wcześniej rozpatrywaliśmy ograniczenie jednostronne: interesowała nas odpowiedź na pytanie, czy badana wartość średnia jest równa p, czy też Hy > H- Przy dwustronnym ograniczeniu granice przedziału ufności spełniają następujące warunki:

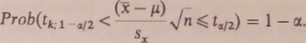
Ponieważ rozkład t jest symetryczny względem 0, czyli t*_;1__a/2 = — t_fca/2, ostatnie wyrażenie można zapisać w postaci:

albo

1

W rzeczywistości rozmiary cząstek tonera podlegają rozkładowi logarytmiczno-normai-nemu, który uzyskuje formę rozkładu normalnego, po przyjęciu logarytmicznej skali na osi poziomej.