fiz (18)

9. BADANIE ZŁOŻENIA

MECHANICZNYCH I ELEKTRYCZNYCH DRGAŃ HARMONICZNYCH POPRZEZ OBSERWACJĘ KRZYWYCH LISSAJOUS

Złożenie drgań w kierunkach wzajemnie prostopadłych

W    przyrodzie    rzadko obserwuje    się proste drgam

harmoniczne. Najczęściej występuje złożenie (nałożenie su ruchów drgających, które różnią się od siebie kierunkar zachodzących drgań, częstotliwościami oraz fazami pocza: kowymi. Gdy drgania składowe odbywają się w tym samym kierunki to mogą występować zjawiska interferencji (lub dudn;

np. rozdziały 8,    29). W niniejszym ćwiczeniu

przypadek złożenia drgań odbywających się w wzajemnie prostopadłych.

Załóżmy, że jedno drganie zachodzi w kierunku osi \XM drugie o tej samej częstotliwości odbywa się w kierunku osi oraz że wyrażamy je wzorami:

x = A sin (Jt

y = B sin (cjt+S),

(9.:

gdzie A, B oznaczają amplitudy tych drgań, o>=2m^=2n/T częstotliwość kołową, ó - różnicę faz między drganiami, częstotliwość drgań, T - ich okres.    fl

Obliczając wielkość sin ut oraz cosut ze wzorów (9.1) podstawiaiac 1e do tożsamości matematycznej

otrzymamy:

+

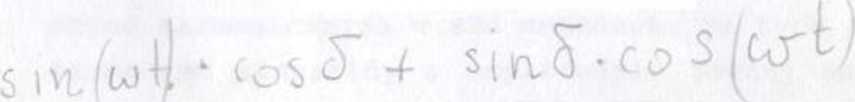
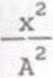
A² y² - 2ABxycos<5 + B²x²cos²S A²B² sin² 6

1.

(9.3)

a no prostych przekształceniach

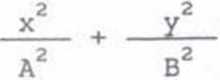
2xycos5

AB

sin² 5.

(9.4)

Wyróżnik tego równania —- —^^S-- =    jest nie mniejszy

A² B² A² B² A B²

od zera. Gdy jest równy zeru, czyli gdy przesunięcie fazowe 5=0 lub 5=71, wówczas równanie (9.4) przyjmuje postać równania prostej y=(B/A)x lub y=-(B/A)x. Gdy wyróżnik równania (9.4) jest dodatni, to równanie to jest równaniem elipsy. W szczególnym przypadku, gdy A=B oraz 5=tt/2 lub 5= 3tt/2, równanie (9.4) staje się równaniem okręgu.

x² + y² = A².    (9.5)

Różnica pomiędzy warunkami 5=tt/2 oraz 5 = 3rr/2 polega na tym, iż w pierwszym przypadku wraz z upływem czasu okrąg jest obiegany zgodnie z ruchem wskazówek zegara (mówimy o obiegu prawostronnym). Natomiast w drugim przypadku okrąg jest obiegany lewostronnie (patrz rys. 9.1).

Warto zauważyć, iż kształt elipsy będącej złożeniem dwóch drgań dostarcza informacji na temat różnicy faz 5 pomiędzy tymi drganiami. Różnicę tę otrzyma się ze wzoru:

5 = arcsin |    (9.6)

lub    5 = arcsin ^    (9.7)

(wielkości a, b, a, fi, X, Y występujące w tym wzorze są zaznaczone na rys. 9.2). Wzór (9.6) nadaje się lepiej do pomiaru dużych wartości 5, natomiast (9.7) do pomiaru małych 6 (poniżej 10°) . Amplitudy wychyleń w kierunku obu osi X i Y nie mają wpływu na wynik pomiaru.