Foto0487

podstawowych rodzajów współczynników korelacji, takich jak: współczynnik korelacji Pearsona r, współczynnik korelacji rangowej Spearmana r, (Kendalla r_k), współczynnik siły związku V Cramera (kontyngencji C).

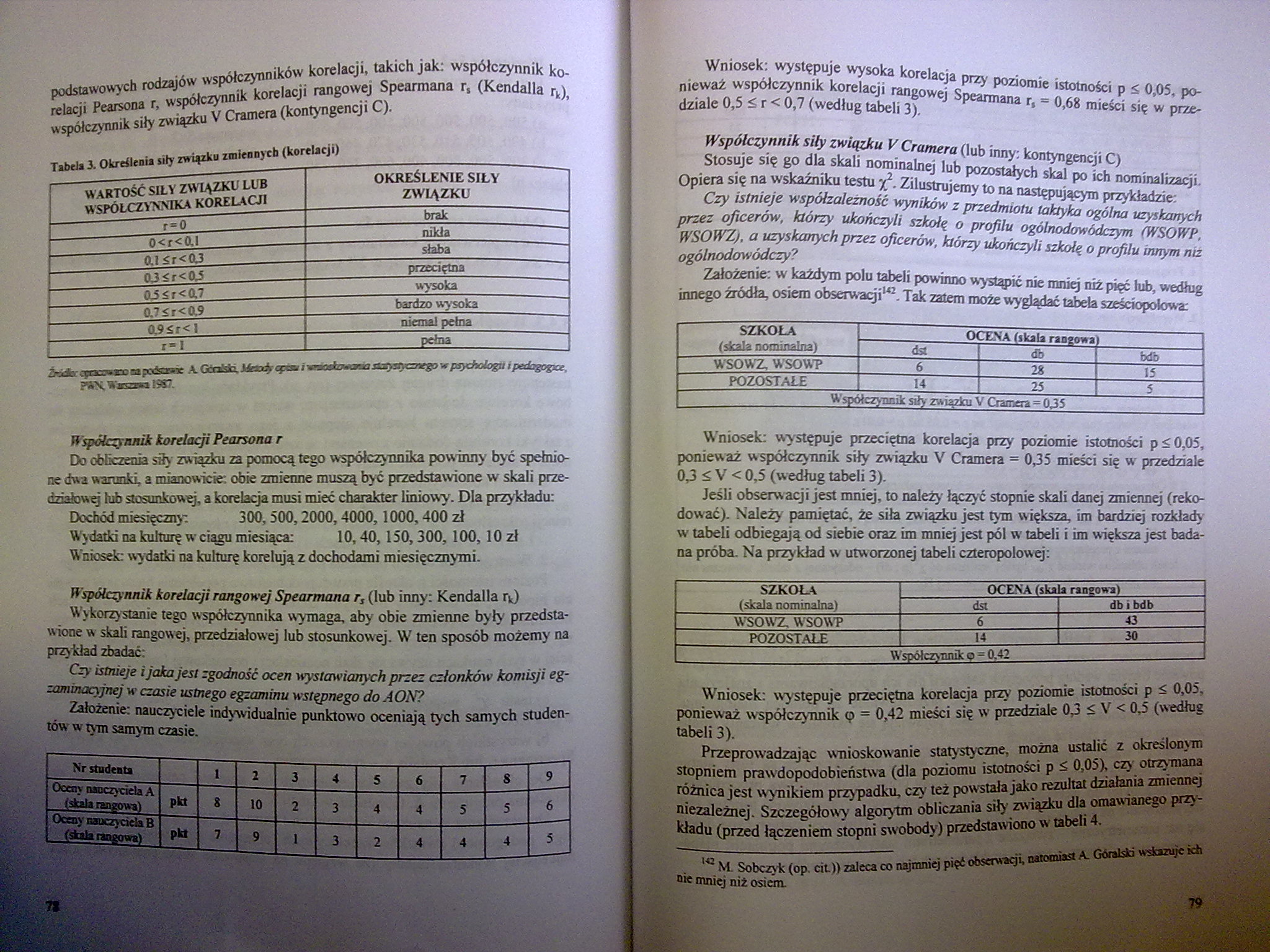
Tabela 3- Określenia siły związku zmiennych (korelacji)

WARTOŚĆ SIŁY ZWIĄZKU LUB WSPÓŁCZYNNIKA KORELACJI	OKREŚLENIE SIŁY ZWIĄZKU
r-0	brak
0<r<0tl	nikła
0ll£r«U	słaba
tUSr<05	przeciętna
<Jt5Sr«t.7	wysoka
0.7Sr<09	bardzo wysoka
0l9£r<l	niemal pełna
r= I	pełna
EWXWKZańt9S7.

Współczynnik korelacji Pearsona r

Do obliczenia siły związku za pomocą tego współczynnika powinny być spełnione dwa warunki, a mianowicie: obie zmienne muszą być przedstawione w skali przedziałowej tub stosunkowej, a korelacja musi mieć charakter liniowy. Dla przykładu;

Dochód miesięczny:    300, 500,2000,4000,1000,400 zł

Wydatki na kulturę w ciągu miesiąca:    10,40,150,300, 100, 10 zł

Wniosek; wydatki na kulturę korelują z dochodami miesięcznymi.

Współczynnik korelacji rangowej Spearmana r_s (lub inny: Kendalla rjJ

Wykorzystanie tego współczynnika wymaga, aby obie zmienne były przedstawione w skali rangowej, przedziałowej lub stosunkowej. W ten sposób możemy na przykład zbadać:

Czy istnieje i jaka jest zgodność ocen wystawianych przez członków komisji egzaminacyjnej w czasie ustnego egzaminu wstępnego do AON?

Założenie; nauczyciele indywidualnie punktowo oceniają tych samych studentów w tym samym czasie.

Nr stndeata		IB9i	2	3	4	S	6	7	8	9
Oceny nacczyciela A (skała rangowa)	pkl	8	10	2	3	4	4	5	5	6
Oceny nauczyciela B (skała rangowa)	pkt	7	9	- J	3	2	4	4	4	5

Wniosek: występuje wysoka korelacja przy poziomie istotności p < 0,05, ponieważ współczynnik korelacji rangowej Spearmana r, = 0,68 mieści się w przedziale 0,5 <, r < 0,7 (według tabeli 3).

Współczynnik siły związku V Crumera (lub inny: kontyngencji C)

Stosuje się go dla skali nominalnej lub pozostałych skal po ich nominalizacji. Opiera się na wskaźniku testu X²- Zilustrujemy to na następującym przykładzie:

Czy istnieje współzależność wyników z przedmiotu taktyka ogólna uzyskanych przez oficerów, którzy ukończyli szkołą o profilu ogólnodowódczym (WSOWP, WSOWZ). a uzyskanych przez oficerów, którzy ukończyli szkołą o profilu innym niż ogólnodowódczy?

Założenie: w każdym polu tabeli powinno wystąpić nie mniej niż pięć łub, według innego źródła, osiem obserwacji¹*². Tak zatem może wyglądać tabela sześciopolowa:

Wniosek: występuje przeciętna korelacja przy poziomie istotności p ś 0,05, ponieważ współczynnik siły związku V Cramera = 0,35 mieści się w przedziale 0,3 ^ V < 0,5 (według tabeli 3).

Jeśli obserwacji jest mniej, to należy łączyć stopnie skali danej zmiennej (reko-dować). Należy pamiętać, że siła związku jest tym większa, im bardziej rozkłady w tabeli odbiegają od siebie oraz im mniej jest pól w tabeli i im większa jest badana próba. Na przykład w utworzonej tabeli czteropolowej:

SZKOŁA (skala nominalna)	OCENA (skala rangowa)
	dst	dbibdb
WSOWZ, WSOWP	6	43
POZOSTAŁE	14	30
Współczynnik © = 0.42

Wniosek: występuje przeciętna korelacja przy poziomie istotności p ś 0,05, ponieważ współczynnik <p = 0,42 mieści się w przedziale 0,3 ^ V < 0,5 (według tabeli 3).

Przeprowadzając wnioskowanie statystyczne, można ustalić z określonym stopniem prawdopodobieństwa (dla poziomu istotności p 1 0,05), czy otrzymana różnica jest wynikiem przypadku, czy też powstała jako rezultat działania zmiennej niezależnej. Szczegółowy algorytm obliczania siły związku dla omawianego przykładu (przed łączeniem stopni swobody) przedstawiono w tabeli 4.

¹⁴² M. Sobczyk (op. ciL)) zaleca co najmniej pięć obserwacji, natomiast A. Góralski wskazuje ich nie mniej niż osiem.

79