HWScan00129

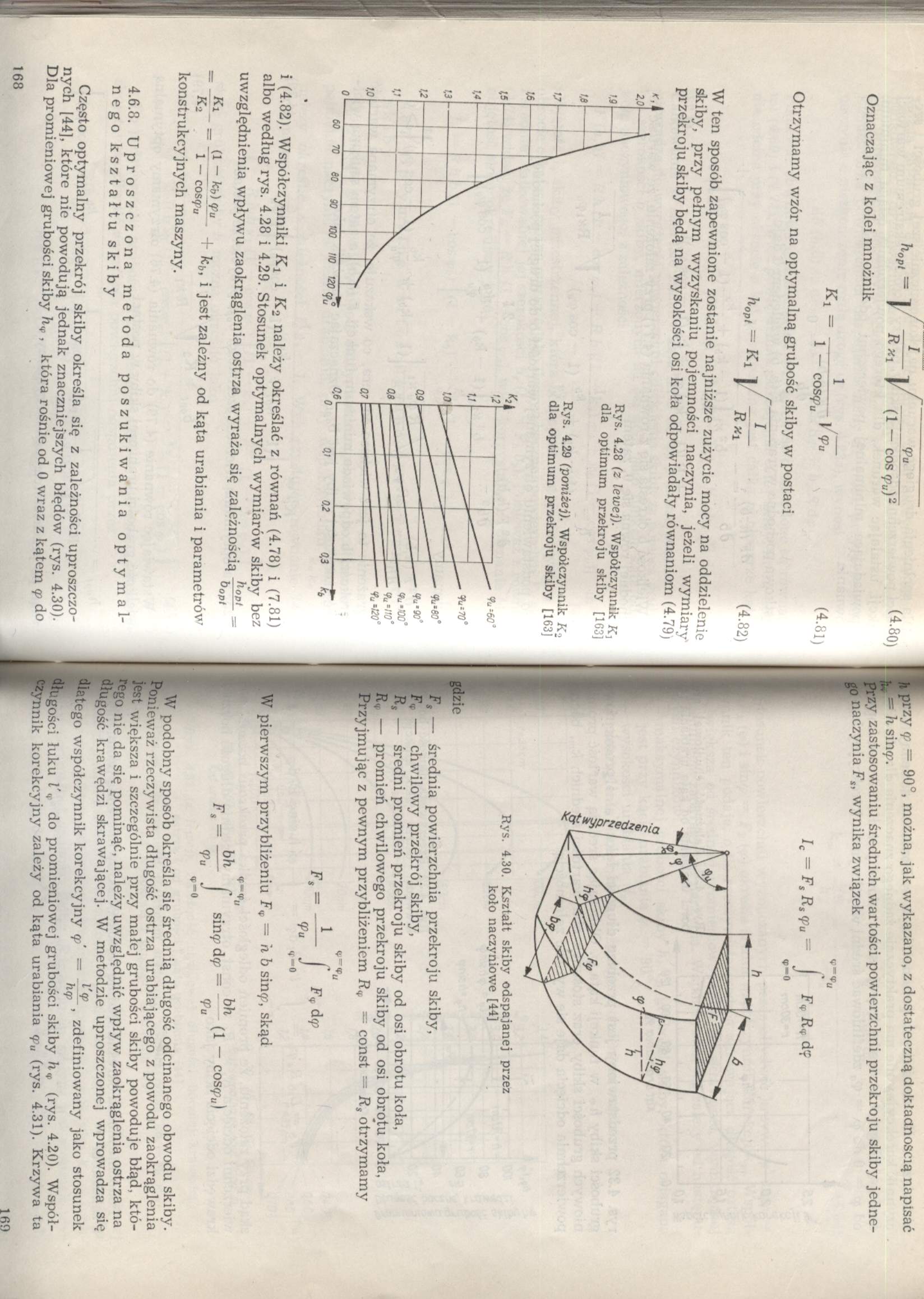
ikV (4.80)

___<Pu__

(1 — COS (fu)'

Oznaczając z kolei mnożnik

Ki = T

V<Pu

1 — COSę>_u

Otrzymamy wzór na optymalną grubość skiby w postaci

(4.81)

(4.82)

h₀pf K i

W ten sposób zapewnione zostanie najniższe zużycie mocy na oddzielenie skiby, przy pełnym wyzyskaniu pojemności naczynia, jeżeli wymiary' przekroju skiby będą na wysokości osi koła odpowiadały równaniom (4.79)

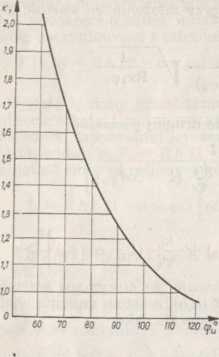
Rys. 4.28 (z lewej). Współczynnik K_} dla optimum przekroju skiby [163]

Rys. 4.29 (poniżej). Współczynnik K₂ dla optimum przekroju skiby [163]

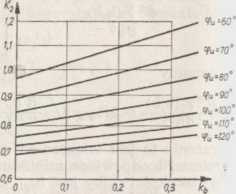
i (4.82). Współczynniki i K₂ należy określać z równań (4.78) i (7.81) albo według rys. 4.28 i 4.29. Stosunek optymalnych wymiarów skiby bez

uwzględnienia wpływu zaokrąglenia ostrza wyraża się zależnością —

—    - + k_b, i jest zależny od kąta urabiania i parametrów

konstrukcyjnych maszyny.

4.6.8. Uproszczona metoda poszukiwania optymalnego kształtu skiby

Często optymalny przekrój skiby określa się z zależności uproszczonych [44], które nie powodują jednak znaczniejszych błędów (rys. 4.30). Dla promieniowej grubości skiby h_v , która rośnie od 0 wraz z kątem (p do

j, przy y — 90°, można, jak wykazano, z dostateczną dokładnością napisać k = h siny.

przy zastosowaniu średnich wartości powierzchni przekroju skiby jednego naczynia F_s, wynika związek

h

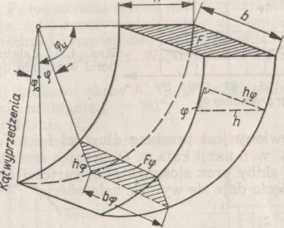
Rys. 4.30. Kształt skiby odspajanej przez koło naczyniowe [44]

gdzie

F_s — średnia powierzchnia przekroju skiby,

F«f — chwilowy przekrój skiby,

R_s — średni promień przekroju skiby od osi obrotu koła,

R_H, — promień chwilowego przekroju skiby od osi obrotu koła. Przyjmując z pewnym przybliżeniem Rą, = const == R_s otrzymamy

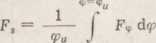
V “0

W pierwszym przybliżeniu F„ = a b siny, skąd

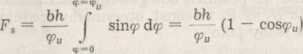
W podobny sposób określa się średnią długość odcinanego obwodu skiby. Ponieważ rzeczywista długość ostrza urabiającego z powodu zaokrąglenia jest większa i szczególnie przy małej grubości skiby powoduje błąd, którego nie da się pominąć, należy uwzględnić wpływ zaokrąglenia ostrza na długość krawędzi skrawającej. W metodzie uproszczonej wprowadza się

dlatego współczynnik korekcyjny y —    , zdefiniowany jako stosunek

długości łuku l\ do promieniowej grubości skiby h_v (rys. 4.20). Współczynnik korekcyjny zależy od kąta urabiania y_u (rys. 4.31). Krzywa ta

169