HWScan00156

Zależność powyższa osiąga minimum, jeżeli

skąd

_dLsu _		Hu	<P» ) = n
d m	v r^m	R	m^2 /
	<P„R _		<Pu
^mopt	I 33 E rić	K(i	- COSqpu)

(4.87)

Podobnie określamy średnią powierzchnię

F_su = F_s Zu

(4.88)

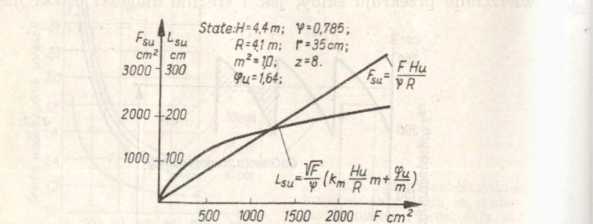
Powierzchnia przekroju skiby

Rys. 4.37. Średnia powierzchnia skiby i średnia długość ostrza w zależności od powierzchni przekroju skiby [44]

FH_U xp R

Rysunek 4.37 przedstawia średnią powierzchnię przekroju skiby i średnią długość skrawającą ostrza w zależności od powierzchni przekroju skiby F = bh. Widzimy, że F_su jest proporcjonalne do powierzchni przekroju skiby, L_su jest proporcjonalne do pierwiastka powierzchni F, pozostałe zaś

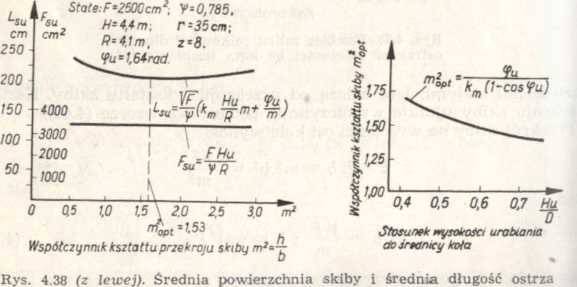
jako funkcja współczynnika kształtu przekroju {44]

Rys. 4.39 (z prawej). Zależność współczynnika kształtu przekroju od stosunku wysokości urabiania i średnicy koła naczyniowego [44]

wielkości wchodzące do wzoru są stałe. Przedstawiając zależności (4.86) funkcji m² otrzymamy przebieg krzywych podany na rys. 4.38. Średnia powierzchnia przekroju F_su jest niezależna od kształtu skiby, podczas gdy jednia skrawająca długość ostrza L_s„ osiąga minimum przy optymalnym stosunku przekroju skiby m- = 1,53. Ta optymalna długość skrawającego ostrza nie występuje przy m² = 1, jak to dotychczas było przyjmowane. Rysunek 4.39 pokazuje przebieg optymalnego m² w zależności od stosunku wysokości urabiania H,_t do średnicy koła D.

4.7. Moc silnika mechanizmu urabiania koparki kołowej jako funkcja jednostkowego powierzchniowego oporu kopania

Ze względu na wykazaną zmienność jednostkowego powierzchniowegc oporu kopania, zależną od grubości skiby, należy dla określenia całkowitej siły kopania zsumować siły obciążające poszczególne naczynia urabiające.

4

Zakładając maksymalną wysokość urabiania H_u = ₃ R, określamy liczbę naczyń chwilowo urabiających przy zastosowaniu kąta urabiania

71    .    .1    71    71    11

<p_u= ^- + arcs.n-₃- = -₂ + — = _*

co odpowiada kątowi cp_u = 110°.

Oznaczając przez z liczbę naczyń na kole, otrzymamy liczbę naczyń

<p z

urabiających z_u = ₃“—, gdzie (p_u w stopniach. Ilości naczyń urabiających w liczbach całkowitych podano w tablicy 4.2.

Tablica 4.2

Liczba naczyń urabiających jako funkcja całkowitej liczby naczyń przy kącie urabiania <p_u = 110°

Liczba naczyń koła z.....	6	7	8	9	10	11	12
Liczba naczyń urabiających zu
rzeczywista......;	2	3	3	3	4	4	4
wartość obliczeniowa . .	2,83	3,14	3,44	3,75	3,75	4,36	4,67

LA i	h		>
1 \ I tu/J		W /tfu/j
Rys. 4.40. Geometria skiby			V
a — pionowej, b — poziomej d)		6J 'Cd	E

Zmienność grubości skiby h w zależności od położenia naczynia przy Urabianiu skibą pionową (rys. 4.40) wyraża się przybliżoną zależnością K — h sin (<p + a). W obliczeniach zwykle zakłada się a = 0 i stąd

h_v — h sin <p    (4.89)

Dla skiby poziomej h* = h sin [ę/_u — (ę? + a)J, przy czym zwykle przyjmuje się