new 57 (2)

116 6. Obliczenia gwintów

w stosunku do pozostałych krzywizn i w związku z tym może być pominięta w obliczeniach. Suma i różnica krzywizn przy wymienionym wyżej uproszczeniu wyraża się wzorami

*e=

4 r — djc

F(e) =

d(c

dk ‘ dk r rd_k ’    * ^łS' 4 r — d_k '

Promień rowka bieżni śruby i nakrętki jest taki sam i wielkość

2 08

jego jest zazwyczaj równa r = 0,520*. Dla takiego promienia Eg

2 COS² Cljc

F(o) = 0,926 oraz    0,415 (jeśli pominie się krzywiznę bieżni———•

to K_1(J= K₂₍₎ —K_a). Podstawiając do wzoru (6.67) Q*(z) = ki(z)dic oraz 2,08

dk

q(z)P

« Di* sin a*

, a także korzystając z przekształconego wzoru (6.64): k,(z) = , otrzymujemy

^V' = ^K'‘V^A(V^L+-^L6T-)^!2'⁰⁸'^,‘

.    ,q*(z). (6.68)

nu_iksma_k I

Przemieszczenie osiowe gwintu śruby i nakrętki w wyniku odkształceń kontaktowych jest równe

<Mz) = ó_łfc(z)+Ó2fc(z) — (Vi + V₂)sinak = T_kq ³ (z),

(6.69)

gjdzie

(6.70)

n - K, Y[2,08<l* -r) śin «.{]/~+ “j.;—)]

2    . 2 \ |2

— Vi    1 — Vk

+

f<2    Ek

Łączne przemieszczenie gwintu w przekroju z zgodmo z zależnością (6.66) i (6.69) opisać można wzorem

(6.71)

ói(z) + (3_z(z) = (5_p(z) + ó*(z) = rq(z) + r*q (z) i stąd równanie przemieszczeń przyjmie postać

^{2 2}‘ 2 Ą Jjq(Zj) dd dz=[rq(z)+r*q^ (z)] - [ Tq(0)+r*q^T (0)].    (6.72)

0 o

Dokładne rozwiązanie tego równania jest bardzo pracochłonne. Dlatego też w praktyoe stosuje się rozwiązania przybliżone. Przybliżenie to polega na linearyzacji rozkładu obciążeń wynikających z odkształceń kontaktowych. Przyjmuje się mianowicie, że

2

(6.73)

q³ (z) = o + bq(z),

gdzie a i b są parametrami stałymi.

Ponieważ rozkład obciążeń w gwincie tocznym jest znacznie bardziej równomierny niż w gwincie zwykłym, a linearyzacja dotyczy tylko jednej, mniejszej ze składowych obciążeń, założenie takie nie prowadzi do dużych błędów.

Uwzględniając wzór (6.73) równanie (6.72) przyjmie postać

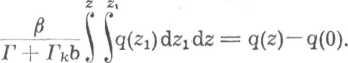
0 0

(6.74)

Jak widać z równania (6.74) parametr a nie ma wpływu na rozkład obciążenia. Parametr b należy zaś tak dobrać, aby aproksymująca prosta pokrywała się ze styczną linii określonej równaniem (6.73) w punkcie Q

q = q*, = -jy- , czyli

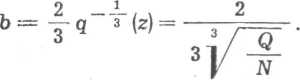
Różniczkując dwukrotnie równanie (6.74), otrzymujemy

(6.75)

q"(z)-m²q(z) = 0,

gdzie

Uwzględniając warunki brzegowe (patrz punkt 6.1.5), otrzymujemy równanie rozkładu obciążeń w gwincie w połączeniu różnoimiennym

Qm

⁹⁽²⁾ sinh mN

coshmz

(6.76)

oraz w połączeniu jednoimiennym

q(z) =

Qm coshmz

sinhmN E₁F₁

coshm(N — z) 1

*₂F₂

(6.77)

Przykładowy rozkład obciążeń w gwincie, w którym wszystkie elementy wykonano ze stali ŁH15 (£ = 2,1-10⁵ MPa, i'= 0,30, HRC = 60) o wymiarach d_p = 100 mm, P — 12 mm, d* = 7 mm, r = 0,52d_k =