71430 new 55

112 6. Obliczenia gwintów

darni praktycznymi, bowiem ścięcie gwintu w nagwintowanym gnieździe jest nie do naprawienia, natomiast usunięcie zerwanej (odprężonej) śruby nie przedstawia dużych trudności. Aby nośność gwintu określona za pomocą siły ścinającej T była większa od nośności rdzenia śruby okre-

r.dl

słonej za pomocą siły Q R™ spełniony musi być warunek

k₂N₀ndRt2 ^ — da R_m,    (6.59)

gdzie N₀ jest wymaganą wysokością nakrętki, a R_m —• doraźną wytrzymałością na zerwanie materiału śruby.

Podstawiając wzór (6.57) do nierówności (6.59), otrzymamy

K,l -+- K_ti    4

stąd

No > ^3 p Rfl + Rt2

d " 4d~^m R_tlR_t2 ■

Dla gwintu metrycznego d₅ = d — 1.0825P, zatem mamy

No

d

(6.61)

Przyjmując zgodnie z hipotezą Hubera R_t2 = 0,58H_m oraz zakładając

d

nieco lepszy materiał śruby R_a — l,25R_t2, dla —= 6 (niewielkich wymiarów gwint zwykły), otrzymujemy

~ > 0,63. d

Wynik ten potwierdza słuszność przyjmowania wysokości nakrętki z gwintem zwykłym H = 0,8d; przy tej wysokości wytrzymałość gwintu jest zapewniona i o wytrzymałości złącza decyduje warunek na zerwanie śruby.

Ze wzoru (6.61) wynika, że wraz ze wzrostem ~ (gwinty drobno-

zwojne) dla zapewnienia wytrzymałości gwintu należy zwiększyć wysokość nakrętki Np.

Wynika stąd wniosek, że silnie obciążone złącza powinny mieć gwinty normalne.

W połączeniach ruchowych wysokość nakrętki oblicza się ze wzoru (6.48). Wielkość nacisków powierzchniowych określonych ze względu na zużywanie się gwintu (ścieranie) jest na tyle mała, że nie ma obaw zniszczenia gwintu przez ścięcie.

6.5. Rozkład obciążenia w gwincie tocznym

Podstawowe parametry geometryczne gwintu tocznego o najczęściej stosowanym zarysie przedstawiono na rys. 6.23.

d

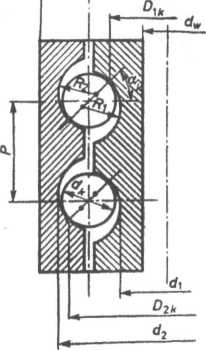
Rys. 6.23. Gwint toczny

Równanie przemieszczeń w przekroju określonym współrzędną z (patrz rys. 6.2) podobnie jak dla gwintów zwykłych ma postać

4(z)+d,(z) = [<Mz) + d₂(z)] - [Ó!<0) - ó₂(0)].

W równaniu tym wskaźnik 1 odnosi się do śruby, a 2 — do nakrętki. Na podstawie równań (6.1), (6.2) i (6.19) sumę przemieszczeń śruby i nakrętki można zapisać następująco:

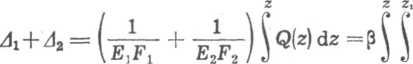
q(z_x) dzi dz.    (6.62)

o    oo

Osiowe przemieszczenia gwintu ó,(z) wynikają z odkształceń 'wywołanych zginaniem d_gi(z), ścinaniem ć>_ti(z), ściskaniem śruby ó_Pi(z) i rozciąganiem nakrętki <5_p2(z) oraz z odkształceń sprężystych na styku kulek z bieżniami (gwintowymi rowkami) śruby i nakrętki d_M(z). Wobec względnie dużego przekroju i jednocześnie małego wysięgu półki gwintu odkształcenia wywołane zginaniem i ścinaniem są bardzo małe i można je bez popełnienia większego błędu pominąć. Głównymi składowymi przemieszczeń są zatem odkształcenia <5_pi(z) oraz <Mz).

Pierwsze z wymienionych wyznaczymy jako funkcję obciążeń liniowych k_t(z) działających na średnicy styku kulek z bieżniami D_ik. Między

• — Połączenia gwintowe