new 56

114 6. Obliczenia gwintów

obciążeniem liniowym k_t(z) i liniowym obciążeniem osiowym gwintu zachodzi relacja

D_lk sina_kcosyk,(z) = q(z)P — Q_P,    (6.63)

gdzie y jest kątem wzniosu gwintu (dla małych kątów wzniosu można przyjąć cosy=l).

Składowa obciążeń liniowych k,(z) w kierunku promienia odniesiona do podziałki gwintu P daje wartość nacisków promieniowych p_r(z)

p,(₂) _ łSBffft. „ SSUg&JO-.    (6.64)

P    7tD|k

Odkształcenie promieniowe śruby u_x na średnicy di zgodnie ze wzorami (6.13) i (6.64) będzie równe

Ul =

d, / dj + cfc \ d{ — dt

\ q(z)ctgait 7 *D_lk

(6.65)

a odkształcenie nakrętki na średnicy D według wzorów (6.14) i (6.64) wynosi

D IdI + d² 2E₂ \D* — D^ł

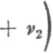
q(z)ctga_fc

xD₂k

Przemieszczenie osiowe gwintu śruby i nakrętki (patrz rys. 6.5) wyraża zależność

ó_p(z) = ópi(z) -1- óp₂(z) = (lą + uijctga* = rq{z),    (6.66)

gdzie

\ D lDz + D² W EjDak - D²

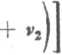
ctgak 2* ‘

d, / d? + dŁ

EiDiłcl dj-dl

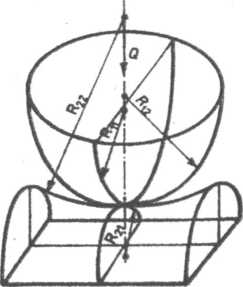
Odkształcenia na powierzchni styku między kulką i bieżnią (w kierunku działania obciążenia na kulkę) wyznacza się ze wzorów Hertza

V, = K_ti

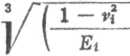
1 -

+

Eh

eQl(z)'

(6.67)

gdzie v_it v_k są współczynnikami Poissona materiału śruby (i = 1), nakrętki (i — 2) i kulki, E,, E_k — modułami sprężystości, Q_k(z) = k_t(z)t_k jest obciążeniem kulki, t_ktad_k — podziałką rozmieszczenia kulek (odległość między sąsiednimi kulkami), Eg — —    - J—h J + ~~ — sumą

Ku K_i2 K₂i K₂₂

głównych krzywizn stykających się ciał (patrz rys. 6.24),    — bez

wymiarowym współczynnikiem zależnym od różnicy krzywizn E(g),

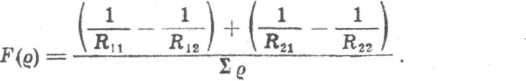
Rys. 6.24. Główne krzywizny styku

F If)

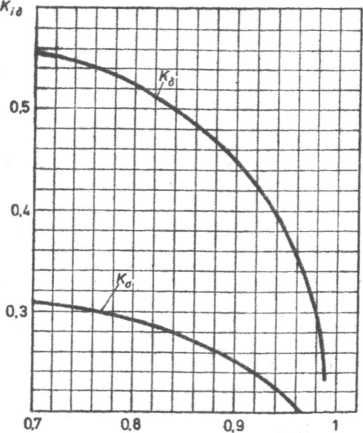
Rys. 6.25. Bezwymiarowy współczynnik odkształceń K_d i naprężeń K_a w zależności

od różnicy krzywizn F, j

Wartości współczynnika K_{. podano na rys. 6.25.

Promienie krzywizn R_tj (i — 1, 2, j = 1, 2) określające zarys powierzchni wypukłych przyjmuje się jako dodatnie, a dla wklęsłych powierzchni

cl*

jako ujemne. Z porównania rysunków 6.23 i 6.24 mamy R_n — R_i2 = —,

Rn~

Pik

2 cos² Ok

(promień koła ściśle stycznego do bieżni w punkcie styku

z kulką), R22 — r. Krzywizna określona promieniem

Pik

2 COS² Ctłc

jest mała