66148 new 44

92 6. Obliczenia gwintów

a

z

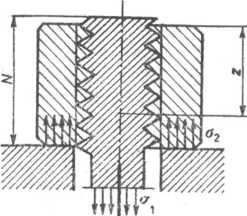
Rys. 6.3. Naprężenia w śrubie i nakrętce

dobnie zmienia się obciążenie ściskające nakrętkę od Q(0) w punkcie D, Q{z) w punkcie F do Q(N) = Q w punkcie F.

Naprężenia rozciągające śrubę o^z) i ściskające nakrętkę o₂(z) (rys. 6.3), przy założeniu równomiernego ich rozkładu w przekrojach poprzecznych śruby Fi i nakrętki F₂ są odpowiednio równe

(6.1)

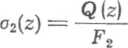
Zgodnie z prawem Hooka wydłużenie śruby dla dowolnej wartości zmiennej z < N będzie równe

Z

o

(6.2a)

i podobnie skrócenie nakrętki

Z

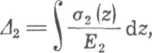
o

(6.2-b)

gdzie Fi i F₂ oznaczają moduły sprężystości podłużnej materiału śruby i nakrętki. Wraz ze wzrostem zmiennej z rośnie obciążenie zwojów. Najmniejsze obciążenie przenoszą zwoje górne, największe zwoje dolne. Różne jest również ugięcie kolejnych zwojów gwintu. Ugięcie zwoju górnego śruby dla z—0 (punkt A na rys. 6.2) jest najmniejsze i wynosi 5i(0), a ugięcie zwoju w punkcie B jest równe <h(z). Analogicznie zwoje nakrętki ugną się o ó₂(0) w punkcie D i o <3₂(z) w punkcie F.

Z łańcucha wymiarowego na rys. 6.2 wynika równość

ó₂(0)+ói(0)+z+A_x=z— A₂+Si (z) + 5₂(z),

6.1. Rozkład nacisków na gwincie w złączu różnoimiennym

93

stąd mamy

Ą+Ą= [di (z) + d,(z)] - [<5,(0) + a₂(0)] •    {6.3)

Ugięcie zwojów d_t(z) (i=1, 2) są efektem zginania i ścinania. W gwintach o roboczym kącie boku a_T 0 występuje dodatkowo przemieszczenie poprzeczne, gdyż na skutek pochylenia płaszczyzny nośnej gwintu pojawia się obciążenie ściskające śrubę i rozciągające nakrętkę. W wyniku przemieszczeń poprzecznych powstaje luz promieniowy a stąd i przemieszczenie osiowe. Odkształcenia wynikające z przewężenia rozciąganych śrub i poszerzenia ściskanych nakrętek są pomijalnie małe i dlatego można ich nie brać pod uwagę.

6.1.2. Odkształcenia wywołane zginaniem gwintu

Odkształcenia wywołane zginaniem gwintu wyznaczyć można z równania różniczkowego

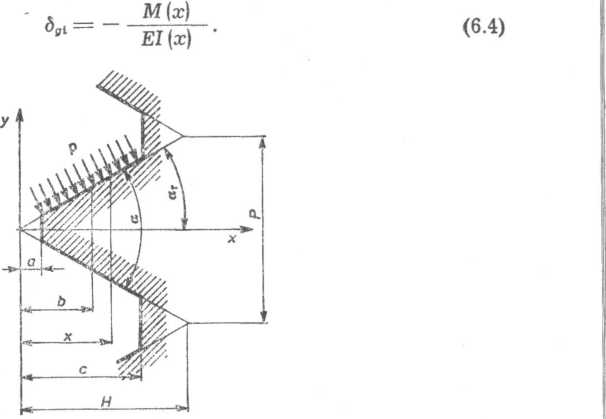
Rys. 6.4. Obciążenie zwoju gwintu

Jeśli przyjmiemy założenie, że naciski p(z) na powierzchni gwintu rozkładają się równomiernie wzduż linii zarysu, moment gnący M{x) działający na półkę gwintu o jednostkowej szerokości wyrazi się wzorem

M[x)=p{z)    -p(z) (x-a)tga_r~^tga_r,

zatem

M(x)

p(~)

[(x—a)²—(x²—a?) tg²a_r].

(6.5)

2