11828 new 46

96 6. Obliczenia gwintów

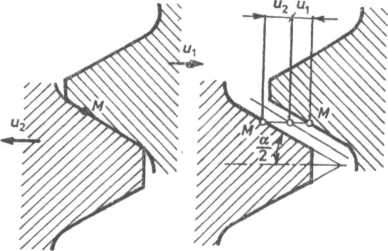
Rys. 6.5. Odkształcenia wynikające z kołowo-symetrycznego ściskania śruby i rozciągania nakrętki

znaczyć wartości promieniowych nacisków p_r(z) działających na walec o wysokości równej podziałce gwintu

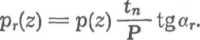
(6.12)

Założenie skokowej zmiany nacisków (co zwój) upraszcza jedynie sposób rozumowania, gdyż wyniki obliczeń przy tym założeniu są również poprawne dla ciągłej zmiany nacisków.

Odkształcenia promieniowe śruby u_: na średnicy di zgodnie z teorią Lamego określa wzór

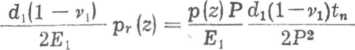
a odkształcenia promieniowe nakrętki u₂ na średnicy D wzór

gdzie D_z jest zewnętrzną średnicą nakrętki (dla nakrętki sześciokątnej należy przyjąć średnicę równoważną, równą w przybliżeniu rozwartości „pod klucz” S, czyli D_z« 1,7D).

W przypadku gdy w śrubie wydrążony jest otwór o średnicy d_w odkształcenie Ui oblicza się ze wzoru

(6.13b)

Przemieszczenie osiowe wyznaczamy (patrz rys. 6.5) z zależności

d_pi(z) = u_ttga_r

(6.15)

6.1. Rozkład nacisków na gwincie w złączu różnoimiennym

97

gdzie

COpl —

di(l n:) tn

tg²Or

Wp2

Dl	+ D-\	D tg^2 ar
Dl	— D*/	2 P*

to bezwymiarowe współczynniki zależne od średnicy nominalnej i skoku gwintu. Dla gwintu metrycznego, dla którego dj = d-1,0825P, t_n — — 0,54125P, a_r = 300, d — D przy n = r₂ = 0,3 otrzymamy

«pi = 0,06315 -^-0,06835; w_p2 =0,3930 ~ .

Łączne przemieszczenia zwojów śruby ói(z) i nakrętki d₂(z) będą równe

<3i(z) = ^i^) + a_tl(z)+ó_pl{z) =^|—w,    (6.16)

oraz

U*) = W + śaW+Wz) =^P~-?co₂,    (6.17)

•ł₂

gdzie oji — Wpi+cun+Wp! i    = w_s2 + a;_t2+co_P2 (dla gwintu metrycznego

d    d

coi = 0,516+0,05315 -p-, cu₂ = 0,758+0,393 -p).

6.1.5. Rozkład obciążenia w gwincie

Na podstawie wzorów (6.2a), (6.2b), (6.16) i (6.17) równanie (6.3) ma postać

S^^d*+$^U=IP(2>-P«>>]

(6.18)

Równanie to można uprościć, wprowadzając pojęcie liniowego obciążenia osiowego q(z) to znaczy obciążenia przypadającego na jednostkę długości złącza. Siłę rozciągającą śrubę lub ściskającą nakrętkę w przekroju z w zależności od liniowego obciążenia osiowego q(z) można wyrazić następująco

Z

Q(z) — 5 q(z)dz.    (6.19)

0

Całkowite obciążenie działające na śrubę wynosi

(6.20)

(6.21)

Q = J q(z)dz,

0

a obciążenie działające na jeden zwój jest równe

Qp ~ J q(z)dz.

7 — Połączenia gwintowe