DSCN1607

114 #. Obliczenia gwintów

obciążeniom liniowym Jc»(s) i liniowym obciążeniem osiowym gwintu za-chodzi relacja

As su\o*cosyki(r) =» q{:)P = Q_P,    (6.63)

gdzie y jest kątem wznio^i gwintu (dla małych kątów wzniosu można przyjąć cosy ** 1).

Składowa obciążeń liniowych k«(z) w kierunku promienia odniesiona do podziałki gwintu P daje wartość nacisków promieniowych p,(z)

(6.64)

^p,W P    nDu,

Odkształcenie promieniowe śruby U| na średnicy di zgodnie ze wzorami (6.13) i (6.64) będzie równe

•■-|Sp-ffj§j    <">

a odkształcenie nakrętki na śrechiicy D według wzorów (6.14) i (6.64) wynosi

D IlA+D' ,    \ q(r)ctgoa

Przemieszczenie osiowe gwintu śruby i nakrętki (patrz rys. 6.5) wyraża zależność

6p(<) = 3,i(z)+óps(=) = (ui+tij)ctga* — rq(z),    (6.66)

gdzie

^r-JpljpT    *■ •

Odkształcenia na powierzchni styku między kulką i bieżnią (w kierunku działania obciążenia na kulkę) wyznacza się ze wzorów Hertza

^Vi=k-iAtt*⁺-4rT^s»«w-    ^<6-⁶⁷⁾

gdzie »•„ są współczynnikami Poissona materiału śruby (i «* 1). nakrętki (i — 2) i kulki, £,, £* — modułami sprężystości, Q»(z) — k,(r)U jest obciążeniem kulki, t*»o’_h — podziałką rozmieszczenia kulek (odległość między sąsiednimi kulkami),    £ i ^    ¹ ^--sumą

głównych krzywizn stykających się ciał (patrz rys. 6.24), K_t* — bezwymiarowym współczynnikiem zależnym od różnicy krzywizn F(g),

*Xe)

(xr~

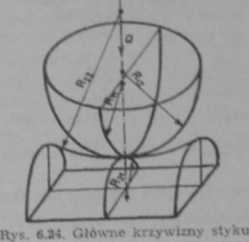
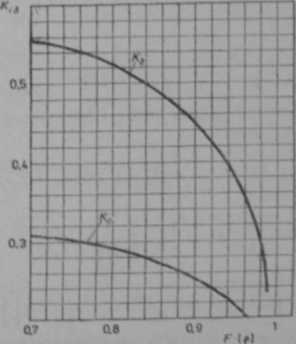
Rys. 6.25. Bezwymiarowy współczynnik odkształceń K₄ 1 naprężeń, K_# w zależności od różnicy krzywizn F_lfi

Wartości współczynnika K,, podano na rys. 6.25.

Promienie krzywizn R_t) (i — 1,2, j - 1,2) określające zarys powierzchni wypukłych przyjmuje się jako dodatnie, a dla wklęsłych powierzchna

_    _ ,, dk

jako ujemne. Z porównania rysunków 6.23 i 6.24 mamy «u * »»“ j •

U *—Q^l*. (promień koła ściśle stycznego do bieżni w punkcie styku ¹    2 cos* aa

z kulką). R_n — r. Krzywizna określona protnieniefn 2cos*«* ^jeSt