DSCN1601

102 S Obliczenia gwintów

i S — i,5a. Jak widać z wykresów dwukrotne zwiększenie wysokości nakrętki powoduje zmniejszenie obciążenia dolnego zwoju % 28"/o do 26,5%.

Przy bardzo dużych obciążeniach wywołujących plastyczną deformację dolnych zwojów gwintu celowe jest stosowanie wyższych nakrętek. Wówczas obciążenie rozkłada się na kolejne zwoje bardziej równomiernie. Przykład przebiegu rozkładu liniowych obciążeń osiowych q(z), przy założeniu odkształceń bez umocnienia plastycznego przedstawia rys. 6.11. W tym przypadku zwiększenie wysokości nakrętki pozwala na przenoszenie większych sil.

6.2. Rozkład nacisków na gwincie w złączu jednoimiennym

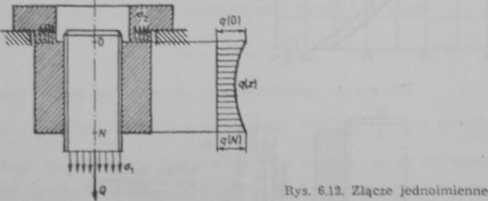
W złączu, w którym zarówno śruba jak i nakrętka są rozciągane (rys. 6.12) równanie przemieszczeń (6.3) ma postać

(i,(«)+3j(2)1 ~MO)+ó_s(0)].

Odkształcenia śruby i nakrętki wyrazić można wzorami

a

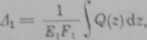
(6.36)

f

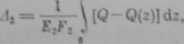
gdzie Q{z) jest siłą rozciągającą śrubę w przekroju s, a Q—Q(z) — siłą rozciągającą nakrętkę w tym samym przekroju. Równanie (6.23) w tym przypadku nu postać

S

t

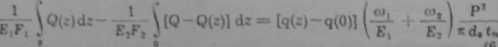
(6.37)

lub, przyjmując oznaczenia takie, jak w p. 6.1.5

P) o w ■^d*    B^r- \q d* - n<i(*)- q(0)l.    (6.38)

• •

Po zróżniczkowaniu powyższego równania otrzymamy

PQ(Z) - -ĘpT Q “ rq’(z)    (6.39)

i po powtórnym zróżniczkowaniu mamy

fiq(*) - rq"(x)    (6.40)

lub przyjmując -jr = m*

q"(z)-ro*q(z) = 0.    (6.41)

Rozwiązanie równania przewidujemy w postaci

q(z) = A sinh mz+B cosh mz.    (6.42)

Stale A i B wyznaczyć można z warunków brzegowych według równania

1 O

(6.39); dla z =» 0 Q(0) = 0 oraz q'(0)*«—„ -= . Ponieważ z równania

I Bjfj

(6.42) mamy q (0) = Am cosh 0 + Bm sinh 0, więc

^A ” ~ Tm K.F,'

Dla z = N Q(N) - Q oraz q'(N) = £ (fi -    - £ jyr.

stąd

B = [q'(JV)—Am cosh mN] - - \    „ =»

^{11 v} '    ¹ m smh mN

Q    I 1    coshmN \

jfm sinh mN \ S,F, ĄFj /"

Zatem równanie (6.42) będzie miało postać

, . Q [7 1    , cosh mN\ cosh mz 1    . ,___] ,_s

lub, podstawiając F = —j-oraz cosh mN cosh m; — sinh mS sinh w; =•

cosh m(N-z),

9(«)

Qm

fi sinh mN

[cosh m;

E_x F,

eoshm(N-z)

F.F,

(6.44)