69278 new 50 (2)

102 6. Obliczenia gwintów

i N = l,5d. Jak widać z wykresów dwukrotne zwiększenie wysokości nakrętki powoduje zmniejszenie obciążenia dolnego zwoju z 28% do 26,5%.

Przy bardzo dużych obciążeniach wywołujących plastyczną deformację dolnych zwojów gwintu celowe jest stosowanie wyższych nakrętek. Wówczas obciążenie rozkłada się na kolejne zwoje bardziej równomiernie. Przykład przebiegu rozkładu liniowych obciążeń osiowych q(z), przy założeniu odkształceń bez umocnienia plastycznego przedstawia rys. 6.11. W tym przypadku zwiększenie wysokości nakrętki pozwala na przenoszenie większych sił.

6.2. Rozkład nacisków na gwincie w złączu jednoimiennym

W złączu, w którym zarówno śruba jak i nakrętka są rozciągane (rys. 6.12) równanie przemieszczeń (6.3) ma postać

Ą~Ą = [0,(2) + d₂(z)] - [5,(0) + ó₂(0)].

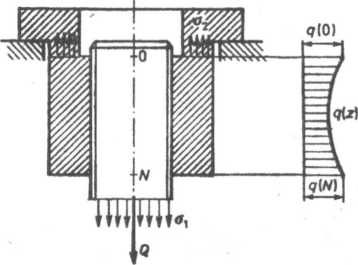
Rys. 6.12. Złącze jednoimienne

Odkształcenia śruby i nakrętki wyrazić można wzorami

Z

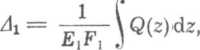
0

(6.36)

Z

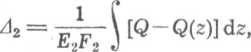
0

gdzie Q(z) jest siłą rozciągającą śrubę w przekroju z, a Q —Q(z) — siłą rozciągającą nakrętkę w tym samym przekroju. Równanie (6.23) w tym przypadku ma postać

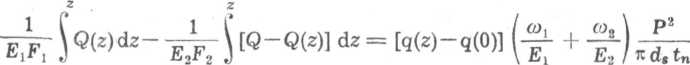
o    o

(6.37)

lub, przyjmując oznaczenia takie, jak w p. 6.1.5

z    z

/?jjQ(z)dz-^^Qdz = r[q(z)-q(0)].    (6.38)

Po zróżniczkowaniu powyższego równania otrzymamy

(6.39)

(6.40)

(6.41)

(6.42)

-Q = r_q'(z)

PQ(z)~

1

E₂Fo

i po powtórnym zróżniczkowaniu mamy

/?q(z) = rq"(z)

lub przyjmując — = ^m“

q "(z) —m²q(z) = 0.

Rozwiązanie równania przewidujemy w postaci

q(z) = A sinh mz+B cosh mz.

Stałe A i B wyznaczyć można z warunków brzegowych według równania

,    1 Q

(6.39); dla z = 0 Q(0) = 0 oraz q (0) =—pr =~=r • Ponieważ z równania

■* JC/2 r 2

(6.42) mamy q'(0) = Am cosh 0 + Bm sinh 0, więc

A =

l Q

Fm E₂F₂ '

Dla * - N Q(N) = Q oraz q'(N) -j-f (fi ■- -j±r) - f j±r-.

stąd

B = [q'(N) — -Am cosh mN]

- ^Q U- +

\EiFi

1

msinh mN cosh mN

An sinh mN Zatem równanie (6.42) będzie miało postać

q (z) =

E₂F₂

)■

f( ^1	, cosh mN\	t cosh mz	1 1
UBjF,	e,f2 1	sinh mN	e2f2 ^sinhmz J

(6.43)

lub, podstawiając N = oraz cosh mN cosh mz — sinh mN sinh mz =

= cosh m(N—z),

Qm [cosh mz , cosh m(N—z)

^q(2)    /? sinh mN L E_lF₁

2^r2

^Ll-

(6.44)