new 47 (2)

98

6. Obliczenia gwintów

Między wielkościami q(z) i p(z) zachodzi związek

(6.22)

Uwzględniając wzory (6.1) i (6.22) równanie (6.18) można zapisać w postaci

Z

[ +'*k] $«*>* =    (f -⁺ ife; ⁽⁶²³⁾

e

lub oznaczając /? =    (podatność śruby i nakrętki) oraz r =

E, F,

P^ł / co, to₂ \

⁵¹ d* tn \ E i    Ej/

E₂ Ej

+ —r²-1 (podatność gwintu) otrzymać Ej /

/?$ Q(z) dz = r(q(z)-q(0)).

0

Po zróżniczkowaniu tego równania względem z mamy

f}Q{z) = rq\z)

i po powtórnym zróżniczkowaniu otrzymamy

(lq(z) = rqⁿ(z).

Stąd

q"(z)—m²q(z) — 0,

,/T * ^m==|/ r

(6.24)

(6.25)

(6.25)

(6.27)

(6.28)

gdzie

jest współczynnikiem bezwymiarowym określającym stosunek podatności śruby i nakrętki do podatności gwintu.

Przebieg zmienności ■& jako funkcji stosunku średnicy nominalnej d

gwintu do podziałki —- (przy Ej = E₂) przedstawiono na rys. 6.6.

Całkę ogólną równania (6.27) można zapisać w postaci q (z) = A sinh mz+B cosh mz,

(6.29)

gdzie A i B są stałymi dowolnymi, które wyznacza się z warunków brzegowych. Mianowicie dla z — 0 mamy sinh mz — 0, cosh mz = 1 oraz

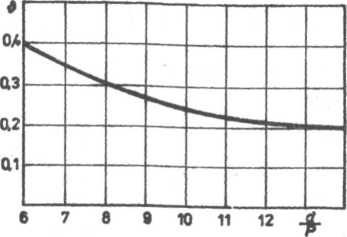
Rys. 6.6. Wykres współczynnika & w zależności od —

P

na podstawie równania (6.25) dla Q(0) = 0 q'(0) = 0. Stąd pochodna równania (6.29) q'(0) — Am cosh mz + Bm sinh mz = Am = 0, czyli A — 0 i całka ogólna upraszcza się do postaci

q(z) = B cosh mz.    (6.30)

Dla z — N q'(N) — Bm sinh mN. Z równań (6.25) i (6.28) mamy q'(N) = = Qm², a zatem

B =

Qm

sinh mN

(6.31)

Ostatecznie równanie rozkładu liniowych obciążeń osiowych przyjmie postać

q(z) =

Qm

sinh mN

cosh mz.

(6.32)

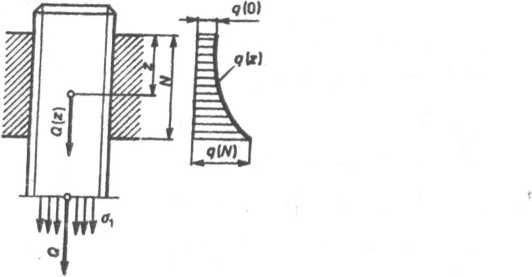
Rys. 6.7. Rozkład liniowych obciążeń osiowych q(z)

Z równania tego wynika, że obciążenia w złączu gwintowym rozkładają się według funkcji cosinus hiperboliczny (rys. 6.7). Największe obciążenie, jakie przenosi dolny zwój (z = N) jest równe