DSCN1599

98 6. Obliczenia gwintów

Między wielkościami q(z) i p(z) zachodzi związek

^P(2,=9(2)SJT-    ^<8-^2s)

Uwzględniając wzory (6.1) i (6.22) równanie (6.18) można zapisać w stad

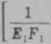
⁺ E,F_t

5«(_Z)dz= [9(=)-9(0>] (-§7 + ^)^

(6.23)

lub oznaczając fi — - ~ - +    — (podatność śruby i nakrętki) oraz JP =-

"l'l Et *2 P* / q>i di] \

= ■ . - l-rr* + -=-) (podatność gwintu) otrzymać

'^tOiin\ C-i fij /

/l[Q(z)dz = r(q(z)-q(0)).    (6.24)

Po zróżniczkowaniu tego równania względem z mamy

/)Q(z) = JY(z)    (6.25)

i po powtórnym zróżniczkowaniu otrzymamy

Stąd

fiq(z) = T q'(z). q"(z)-m*q(z) = 0,

(6.25)

(6.27)

m =    (6.28)

gdzie

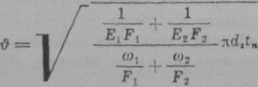
jest współczynnikiem bezwymiarowym określającym stosunek podatności śruby i nakrętki do podatności gwintu.

Przebieg zmiennośd d jako funkcji stosunku średnicy nominalnej

gwintu do podziałki -rp (przy Ej = E,) przedstawiono na rys. 6.6.

Całkę ogólną równania (6.27) można zapisać w postaci

q(z) == A sinh mz+ B cosh mz,    (6.29)

gdzie A i B są stałymi dowolnymi, które wyznacza się z warunków brzegowych. Mianowicie dla z — 0 mamy sinh mz = 0, cosh mz = 1 oraz

P

na podstawie równania (6.25) dla Q(0) = 0 q'(0) = 0. Stąd pochodna równania (6.29) g'(0) = Am cosh mz+Bm sinh mz = Am = 0, czyli A = Q i całka ogólna upraszcza się do postaci

q(z) = B cosh mz.    (6.30)

Dla z = N q’(N) = Bm sinh mN. Z równań (6.25) i (6.28) mamy q'(N) = = Qm*_f a zatem

Ostatecznie równanie rozkładu liniowych obciążeń osiowych przyjmie postać

^,<I,“sfeł^00d”^B2-    <*^Jł)

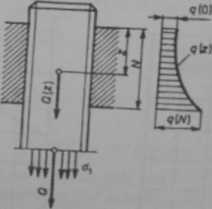
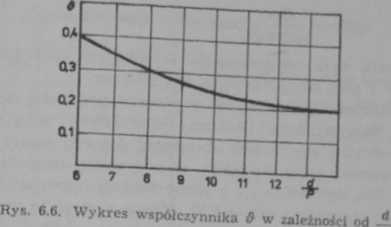
Rys. 6.7. Rozkład liniowych obciążeń osiowych q(z)

Z równania tego wynika, że obciążenia w złączu gwintowym rozkładają się według funkcji cosinus hiperboliczny (rys. 6.7). Największe obciążenie, jakie przenosi dolny zwój (z = N) jest równe