new 54 (2)

110

6. Obliczenia gwintów

Jeżeli porównamy gwinty o jednakowym zarysie a różnych podział-kach Pi i P₂ (rys. 6.20), to okaże się, że gwinty te przy takiej samej średnicy di i jednakowej długości skręcenia mają taką samą wytrzymałość. Zachodzi bowiem zależność: gwint drobnozwojny ma tyle razy dłuższą półkę b — jidjn niż gwint grubozwojny, ile razy ma mniejszą grubość g i wysięg t„/2; stąd zarówno naprężenia gnące według wzoru (6.49) jak i naprężenia skręcające według wzoru (6.50) będą takie same. Takie same w niewielkim przybliżeniu będą również naciski powierzchniowe. Ponieważ jednak rozkład obciążeń w gwincie jest tym bardziej nierównomierny im więcej zwojów ma gwint; w tym kontekście mniejszą wytrzymałość ma gwint drobnozwojny.

6.4. Obliczenia wysokości nakrętki

Połączenie śrubowe obciążone siłą osiową może ulec zniszczeniu bądź, przez zerwanie rdzenia śruby, bądź też przez ścięcie gwintu poprzedzone plastyczną deformacją zwojów (rys. 6.21). Przy normalnej wysokości na

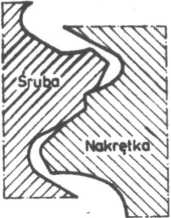
Rys. 6.21. Plastyczna deformacja zwojów gwintu w chwili poprzedzającej ścięcie

krętki N = 0,8d z reguły zniszczenie następuje przez zerwanie śruby. Ścięcie zwojów może więc występować tylko w gwincie drobnozwojnym przy małej grubości nakrętki. Wytłumaczyć to można tym, że śruba z gwintem drobnozwojnym o takiej samej średnicy znamionowej jak śruba z gwintem zwykłym ma większą powierzchnię przekroju poprzecznego. Poza tym rozkład nacisków ńa gwincie drobnozwojnym jest bardziej nierównomierny i w związku z tym deformacje poprzeczne śruby i cienkiej nakrętki, mogą być na tyle duże, że najbardziej obciążone zwoje całkowicie przestają wzajemnie zachodzić na siebie. Zwiększenie wysokości nakrętki w niewielkim tylko stopniu poprawia sytuację. Dlatego też nie zaleca się stosować gwintów drobnozwojnych w silnie obciążonych złączach.

Materiały, z których wykonuje się śrubę i nakrętkę (gwintowane gniazdo), mają na ogół różne własności wytrzymałościowe. Doraźna wy-6.4. Obliczenia wysokości nakrętki

111

trzymałość na ścinanie materiału śruby R_n jest przeważnie wyższa niż wytrzymałość materiału nakrętki R_t2. W związku z powyższym średnica d, na jakiej zachodzi ścięcie gwintu (rys. 6.22) jest większa niż średnia średnica robocza d_s.

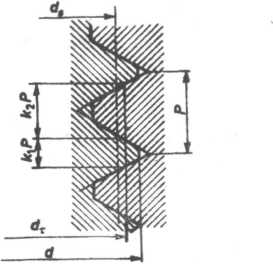
Rys. 6.22. Ścinanie gwintu na średnicy d_t

Z warunku, że siła ścinająca gwint śruby T = nd_t kiPR_tl jest równa sile ścinającej gwint nakrętki T = hd_tk₂PR_i2 wynika równość

klRti — 7C2^t2*	(6.54)
Ponieważ (patrz rys. 6.22)
kiP+k2P = P,	(6.55)
więc z równań (6.54) i (6.55) otrzymujemy
k, — ^R,i 1 Ra + Ra	(6.56)
oraz
ka — ^ Rtl + R„’	(6.57)
Dla gwintu metrycznego i dowolnych skojarzeń	materiałów śruby

i nakrętki wartość ki powinna zawierać się w przedziale — <ki < Jeśli wartość kj obliczona ze wzoru (6.56) jest mniejsza od^-, to ścinany

O

jest tylko gwint nakrętki.

Średnica na jakiej zachodzi ścinanie (patrz rys. 6.22) jest równa

d_; = d_s

2 k.

P.

2 tg

(6.58)

Nie popełnimy większego błędu, jeśli przyjmiemy d_t — d.

Pożądane jest, aby wytrzymałość gwintu na ścinanie była większa od wytrzymałości na zerwanie rdzenia śruby. Podyktowane jest to wzglę-