DSCN1602

104 6. Obliczenia gwintów

Brzegowe wartości q(0) i q(N) (patrz rys. 6.12) będą równe

9(0) =	Qm	/ 1 ,	cosh mN \	(645)
	/JsdnhmN	U,F, ^1	ExFt /’
q(N) =	Qm 1	( cosh mN	,1 }
	~psinhmN '	i ElFl	* EtFtl'

W zależności od podatności elementów połączenia maksymalne obciążenie może wystąpić dla z = 0 lub dla z = N. Z równań (6.45) i (6.46) wynika równanie

•» -    --jdrsT (Sr 1    <^{cosh mW}^| ^<M7>

Ponieważ cosh mN > 1, q(0) będzie większe od q(N), gdy podatność nakrętki będzie większa od podatności śruby 9; - - . W przypadku

ojfJ    "1*1

równych podatności wykres q(z) będzie symetryczny a rozkład obciążeń najbardziej korzystny.

Uzyskanie zupełnie równomiernego obciążenia jest możliwe tylko wtedy, gdy przekroje jednoimiennie obciążonych elementów maleją liniowo do zera w miarę spadku obciążenia w tych przekrojach (rys. 6.13). Aby uzyskać liniową zmienność przekrojów, średnica zewnętrzna nakrętki D_t(z) i średnica wewnętrzna śruby d_K(z) powinny zmieniać się zgodnie z równaniami:

(przy założeniu E_x — £,). Taki przebieg zmienności ze względów technologicznych, nie jest do przyjęcia. Dlatego też w praktyce stosuje się połączenia z liniową zmianą średnic (rys. 6.14). Rozkład nacisków w tym przypadku tylko nieznacznie odbiega od rozkładu równomiernego.

fi-2- WozMad nacisków na gwincie w złączu jednolmiennym

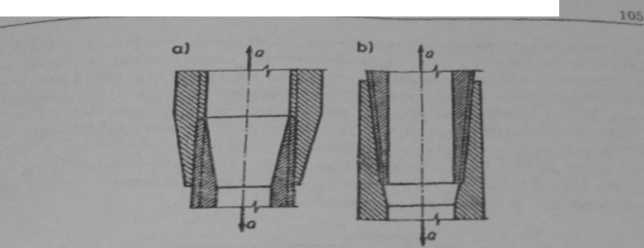
Ry*. 6.14. Ianiowozmienne średnice przekroju (wintu wewnętrznego i zewnętrznego: a) złącze jedno-imienne, b) złącze rurowe z gwintem stołkowym

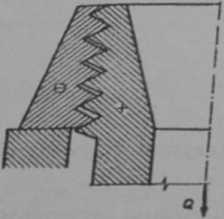
Rys. 6.35. Złącze różnoimien-ne o stałej podzialee jednego gwintu (zewnętrznego) i zmiennej podzialee drugiego gwintu (wewnętrznego)

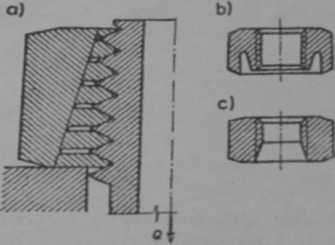
Rys. 6.16. Częściowe upodatnienie złącz ró ino imiennych przez; a) zróżnicowanie głębokości nacięć gwintu nakrętki (nakrętka Sol ta), b) odciążenie dolnych zwojów, c) stożkowe ścięcie dolnych zwojów nakrętki

W połączeniach różnoitniennych zmniejszenie nie równomierności nacisków można uzyskać jedynie przez wykonanie gwintu śruby o nieco mniejszej podzialee od gwintu nakrętki, przy czym poprzeczne przekroje śruby i nakrętki powinny również zmniejszać się liniowo w miarę spadku obciążenia (rys. 6.15). Takie wykonanie gwintu znalazło zastosowanie w zamkach komory nabojowej dział artyleryjskich.

Zmienną podatność gwintu, a przez to częściowe wyrównanie nacisków można osiągnąć także przez zróżnicowanie głębokości nacięć w bruzdach gwintu (rys. 6.16), bądź też przez stożkowe ścięcie nakrętki. Pierwszy