DSCN1609

118 6. Obliczenia gwintów

= 3,64 mm, D« = 95,05 mm, = 104,95 mm, d_w = 70 mm, D, = = 130 mm, N — 72 mm, a_k = 45° przy obciążeniu Q = 72 kN przedstawiono na rys. 6.26.

118 6. Obliczenia gwintów

<łU)

*

u

1 2 3 4 5 6 7 6

Rys. 6.26. Rozkład obciążeń q(z) w gwincie tocznym: 1 — złącze jednoimienne, 2 — złącze różnoimienne

6.6. Obliczenia wytrzymałościowe gwintu tocznego

Gwint toczny przenoszący duże obciążenie podlega procesowi zmęczeniowego niszczenia. Na powierzchni gwintu i na kulkach po .pewnym czasie eksploatacji pojawiają się drobne pęknięcia. Pęknięcia te rozwijając się prowadzą do wykruszenia materiału współpracujących elementów. Zdeformowany styk i wykruszone cząstki materiału bardzo znacznie pogarszają dokładność przylegania, co prowadzi do dużych lokalnych przeciążeń i w efekcie końcowym do szybkiego awaryjnego zniszczenia. Proces ten nosi nazwę pittingu. Aby trwałość gwintu była dostatecznie duża, nactóki stykowe p_m„ wyznaczane ze wzorów Hertza nie powinny przekroczyć wartości doświadczalnie określonych nacisków dopuszczalnych pdop- Warunek ten wyraża nierówność

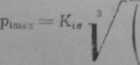
y

C

1 — »? . 1 — r* Ei    E_k

(6.78)

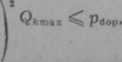
gdzie K|₀ jest współczynnikiem bezwymiarowym zależnym od różnicy krzywizn F[g) (rys. 6.25), a

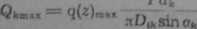
— maksymalnym obciążeniem kulki.

■MMI

Wartości nacisków dopuszczalnych określa się w zależności od twardości stykających się dal. Dla stali ŁH15 o twardości HRC = 60, z jakiej zazwyczaj wykonywane są gwinty toczne, dla normalnej eksploatacji przyjmuje się p«jop == 2500-1-3000- MPa. Przy krótkotrwałej pracy gwintu można przyjąć pd_OP = 4000 MPa. Gdy materiał elementów stykowych ma mniejszą twardość (HRC < 60), wartości nacisków dopuszczalnych określa się z zależności

Pdop = (2500-i-3000)k_p MPa.

Wartości współczynnika k_p podano w tablicy 6.2.

Tablica 6.2. Wartości współczynnika nacisków dopuszczalnych w gwintach tocznych

Twardość materiału elementów stykowych sztywnych HRC	58	54	49	45	40	35	29
kp	0,89	0.79	0,69	0,6	0,5	0,41	0,38